Question

Розв'яжіть задачу, яка прикріплена нижче

Answer 1

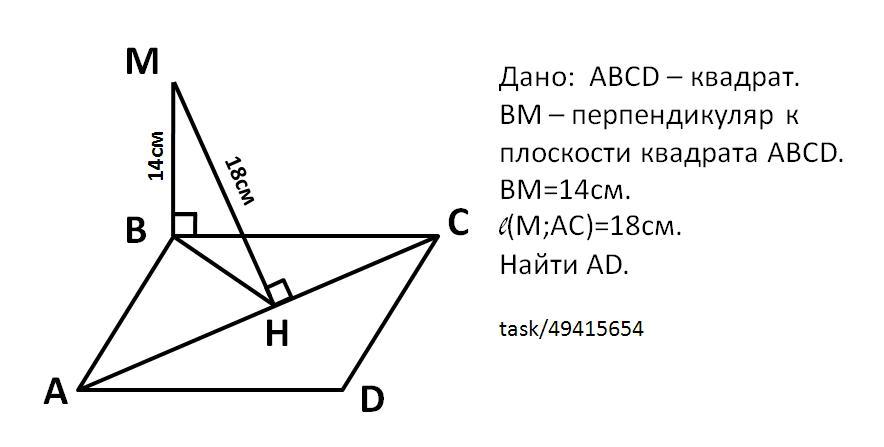
Через вершину В квадрата ABCD проведено перпендикуляр ВМ к плоскости квадрата, длина которого равна 14см. Расстояние от точки М до прямой АС равно 18см. Найти сторону квадрата.

Ответ:

Сторона квадрата равна 16см.

Объяснение:

Проведём АС - диагональ квадрата и МН⊥АС.

Расстояние от точки до прямой - перпендикуляр, опущенный с этой точки на прямую ⇒ l(M;AC)=МН=18cм.

ВМ - перпендикуляр, МН - наклонная, ВН - проекция наклонной, МН⊥АС ⇒ ВН⊥АС (по теореме о трёх перпендикулярах).

По свойству диагоналей квадрата, АС⊥BD.

АС⊥BD, ВН⊥АС ⇒ Н - точка пресечения диагоналей.

Отрезки полученные при пресечении диагоналей равны, следовательно BH = HD.

Рассмотрим ΔBMН.

ВМ⊥(АВС), ВН принадлежит (АВС) ⇒ВМ⊥ВН, ΔBMН - прямоугольный.

По теореме Пифагора:

$\Large \boldsymbol {} MH^2=BM^2+BH^2 \Longrightarrow BH=\sqrt{MH^2-BM^2}=\\\\=\sqrt{18^2-14^2} =\sqrt{128} =\sqrt{64*2} =8\sqrt{2}$

BH=HD, BD=BH+HD⇒BD=2BH=2*8√2=(16√2)см.

Мы нашли длину диагонали квадрата - BD=(16√2)см.

Формула нахождения диагонали квадрата:

$\Large \boldsymbol {} d=a\sqrt{2} \Longrightarrow a=\frac{d}{\sqrt{2} }$

где d - диагональ, а - сторона квадрата. Подставим наши значения:

$\Large \boldsymbol {} AD=\frac{BD}{\sqrt{2} }=\frac{16\sqrt{2}}{\sqrt{2}} =16$

AD = 16cм.