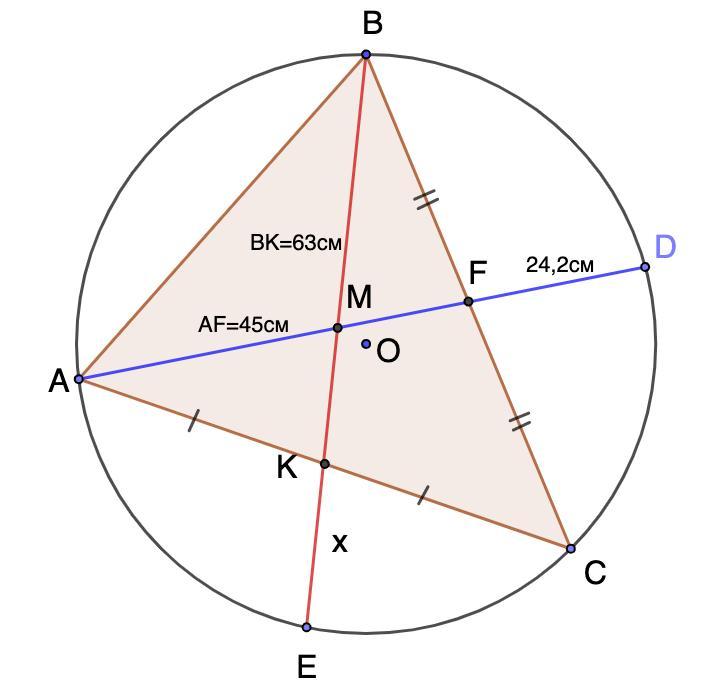
В окружность вписан треугольник ABC, в котором проведены медианы AF и BK. Медиану AF продлили до пересечения с окружностью в точке D. Найдите стороны AC и BC, если BK=63 см, AF=45 см, FD=24,2 см.
Ответы
Ответ:
Стороны АС и ВС равны 42 см и 66 см соответственно.
Пошаговое объяснение:
В окружность вписан треугольник ABC, в котором проведены медианы AF и BK. Медиану AF продлили до пересечения с окружностью в точке D. Найдите стороны AC и BC, если BK = 63 см, AF = 45 см, FD = 24,2 см.
Дано: Окр.О;
ΔАВС - вписанный;
AF и BK - медианы;
AF ∩ Окр.О = D;
BK = 63 см, AF = 45 см, FD = 24,2 см.
Найти: AC и BC.
Решение:
1. ВС ∩ AD = F - хорды.
- Если две хорды пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой.
⇒ AF · FD = BF · FC
BF · FC = 45 · 24,2
BF · FC = 1089
BF = FC (AF - медиана)
⇒ BF = FC = √1089 = 33 (см)
ВС = 66 см.
2. AF ∩ BK = M - медианы.
- Медианы треугольника пересекаются в одной точке и делятся ей в отношении 2 : 1, начиная от вершины.
AF = 45 см ⇒ АМ = 30 см; MF = 15 см.
ВК = 63 см ⇒ ВМ = 42 см; МК = 21 см.
3. AD ∩ BE = M - хорды.
⇒ АМ · МD = BM ·ME
Пусть КЕ = х см
Тогда получим:
30 · (15 + 24,2) = 42 · (21 + х)
1176 = 882 + 42х
42х = 294
х = 7
КЕ = 7 см.
4. АС ∩ ВЕ = К - хорды.
АК · КС = ВК · КЕ
АК · КС = 63 · 7
АК = КС (ВК - медиана)
АК = КС = √441 = 21
⇒ АС = 42 см.
Стороны АС и ВС равны 42 см и 66 см соответственно.
#SPJ1