Question

Сроочноо!
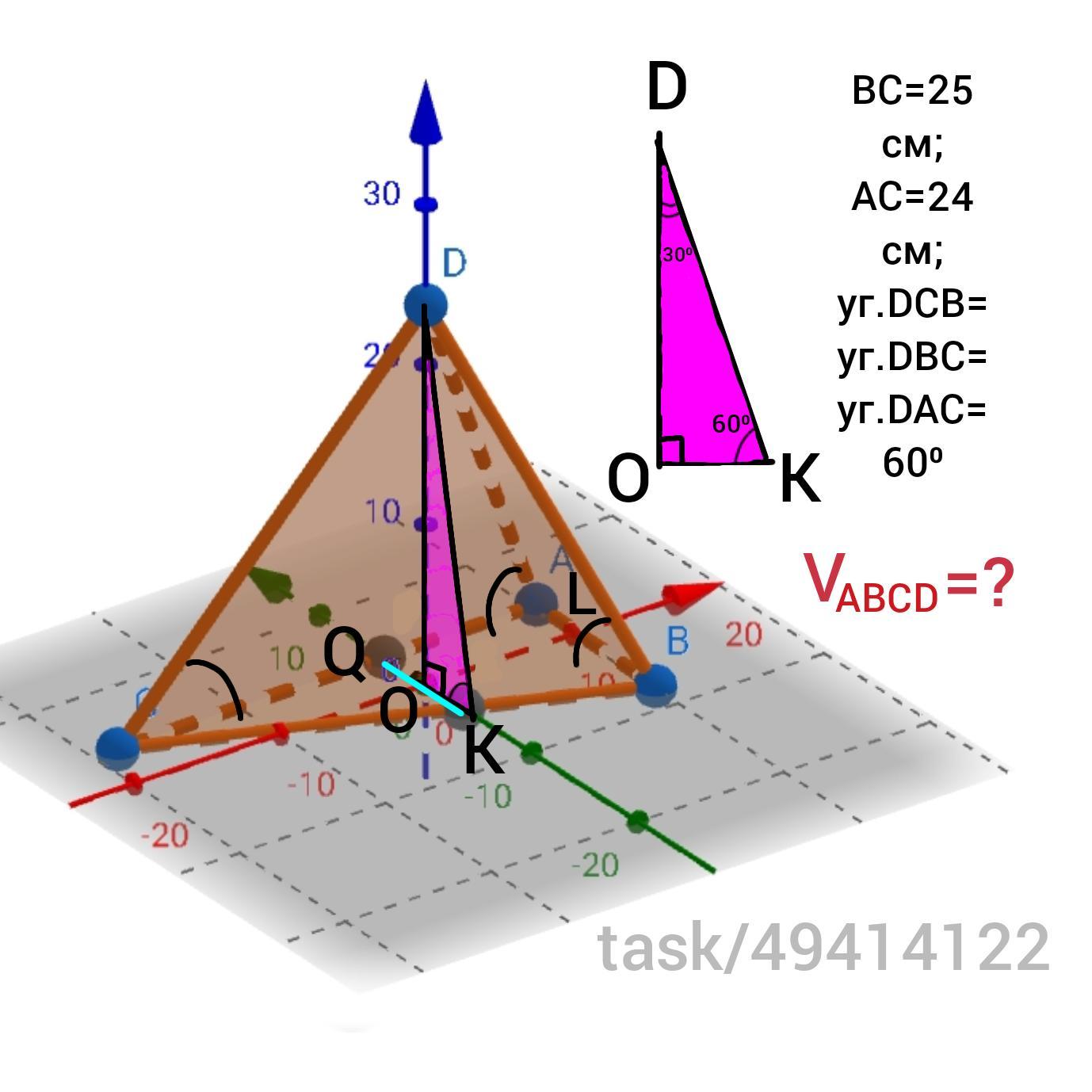
Основою піраміди є прямокутний трикутник із катетом 24 см і гіпотинузою 25 см. Усі бічні грані піраміди нахилені до основи під кутом 60°. Знайдіть об'єм піраміди.​

Answer 1

Ответ:

объем пирамиды составляет $28\sqrt{9,1875} sm^3$

Объяснение:

• найдем катет $AB$ основания пирамиды по теореме Пифагора: $BC^2=AB^2+AC^2;\\AB^2=BC^2-AC^2;\\AB=\sqrt{BC^2-AC^2} ;\\AB=\sqrt{625sm^2-576sm^2} =\sqrt{49sm^2} =7sm;$
• отложим от стороны $AB$ основания пирамиды среднюю линию $QK$,она будет ей параллельна и равна одной второй части: $QK=AB/2=7sm/2=3,5sm;$
• найдем высоту пирамиды, выделив $\Delta DOK$ и найдя в нем катет $DO$.для этого вычислим $\measuredangle D=180^\circ-90^\circ-60^\circ=30^\circ$.катет,лежащий против угла в $30^\circ$,равен половине гипотенузы,следовательно, $OK=3,5sm/2=1,75sm=1/2DK$ и $DK=2OK=1,75sm*2=3,5sm$. теперь,снова воспользовавшись теоремой Пифагора,можно найти высоту пирамиды $DO$: $DK^2=OK^2+DO^2;\\DO^2=DK^2-OK^2;\\DO=\sqrt{DK^2-OK^2} ;\\DO=\sqrt{(3,5sm)^2-(1,75sm)^2} ;\\DO=\sqrt{12,25sm^2-3,0625sm^2} =\sqrt{9,8175} sm;$
• найдем площадь основания пирамиды,прямоугольного треугольника $ABC:$ $\displaystyle S_{\Delta ABC}=\frac{AB*AC}{2} =\frac{\not24sm*7sm}{\not2} =12sm*7sm=84sm^2;$
• вычислим объем пирамиды, он равен одной третьей части произведения ее высоты на площадь основания: $\displaystyle V_{ABCD}=\frac{1}{3} *DO*S_{\Delta ABC}=\frac{1}{\not3} *\not84sm^2*\sqrt{9,1875}sm =28sm^2*\sqrt{9,1875} sm= 28\sqrt{9,1875} sm^3$