Предмет: Геометрия,
автор: izmailsnc
Геометрия каноническое уравнение
Приложения:
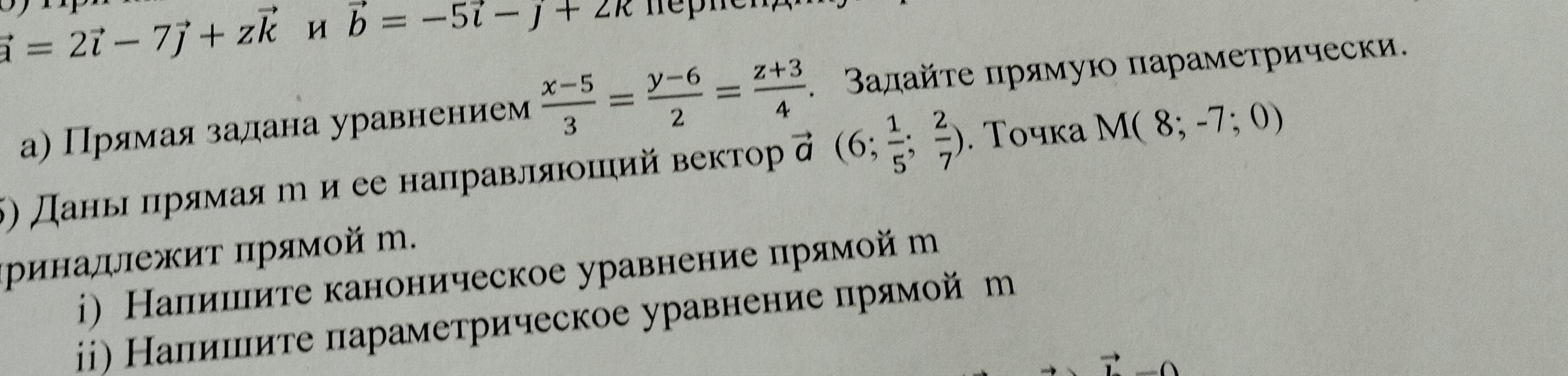
Ответы
Автор ответа:
0
Объяснение:
а) написать данное уравнение прямой так:
тогда параметрический вид будет таким:
б) общий вид канонического уравнения прямой при известном направляющем векторе выглядит так:
после подстановки координат точки М:
параметрический вид этой прямой будет таким:
Похожие вопросы
Предмет: Технология,
автор: NikaCat2005
Предмет: Русский язык,
автор: rzaewagyunai
Предмет: Окружающий мир,
автор: КлевыйБратан
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: v1tal1k777