Question

срочно пж....... 50 бал............​

Answer 1

Ответ:

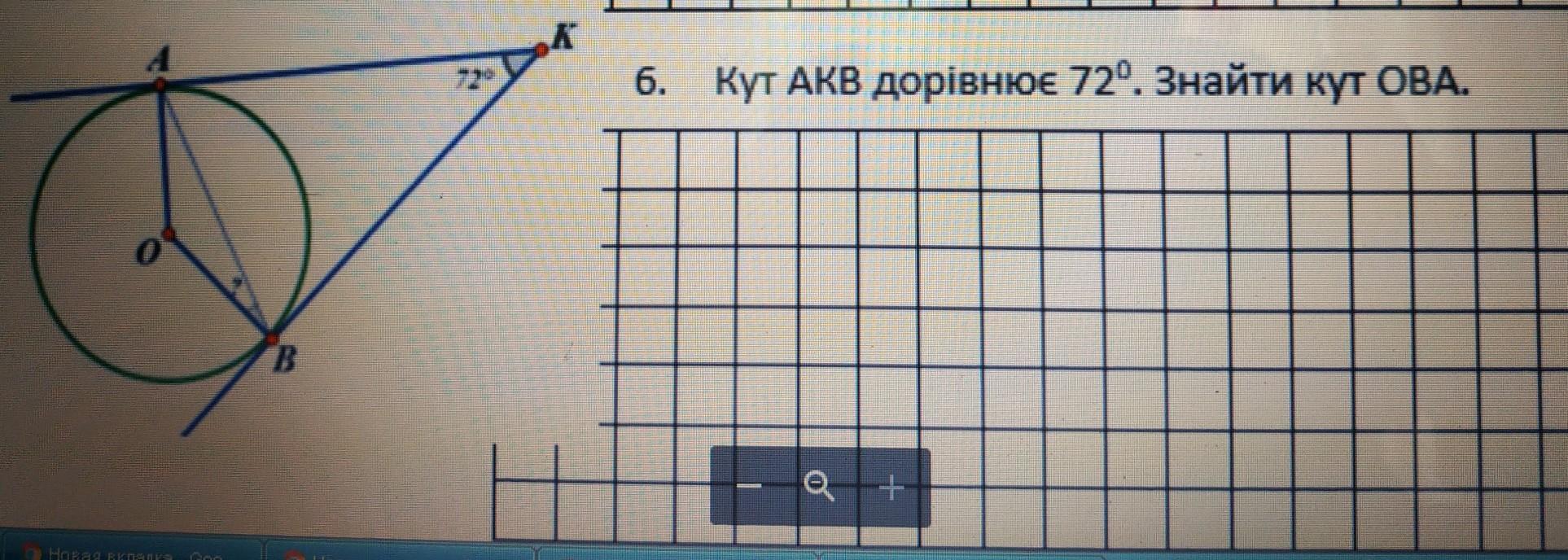
т.к. КА и КВ - касательные к окружности, то

∠ОАК=∠ОВК=90°

Сумма углов правильного четырехугольника - 360°

тогда

∠АОВ + ∠АКВ + ∠ОАК+∠ОВК=360°

∠АОВ + 90 + 90 + 72 = 360

∠АОВ = 108°

ОА = ОВ = r (радиусы окружности) ⇒ треугольник АОВ - ранобедренный⇒ ∠ОАВ=∠ОВА = (180-АОВ):2 = (180-108):2 = 72:2 = 36°

Answer 2

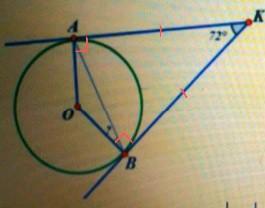
• По свойству касательных - отрезки касательных, проведённых из одной точки, равны .
• Следовательно АК=ВК , отсюда и заметно , что △АКВ-равнобедренный. У равнобедренного треугольника - углы при основании равны (∠А=∠B).
• Сумма углов треугольника равна 180°-ам.
• $\frac{180 {}^{ \circ} - 72 ^{ \circ}}{2} = \frac{108^{ \circ}}{2} = \bf54^{ \circ}$
• Значит ∠А=∠В=54°.
• Угол образовавщийся между радиусом и касательными равен 90°-ам.
• Следовательно ∠ОВА=90°-54°=36°

Ответ: $\bf36^{ \circ}$