СРОСЧНО ДАЮ 100 балів
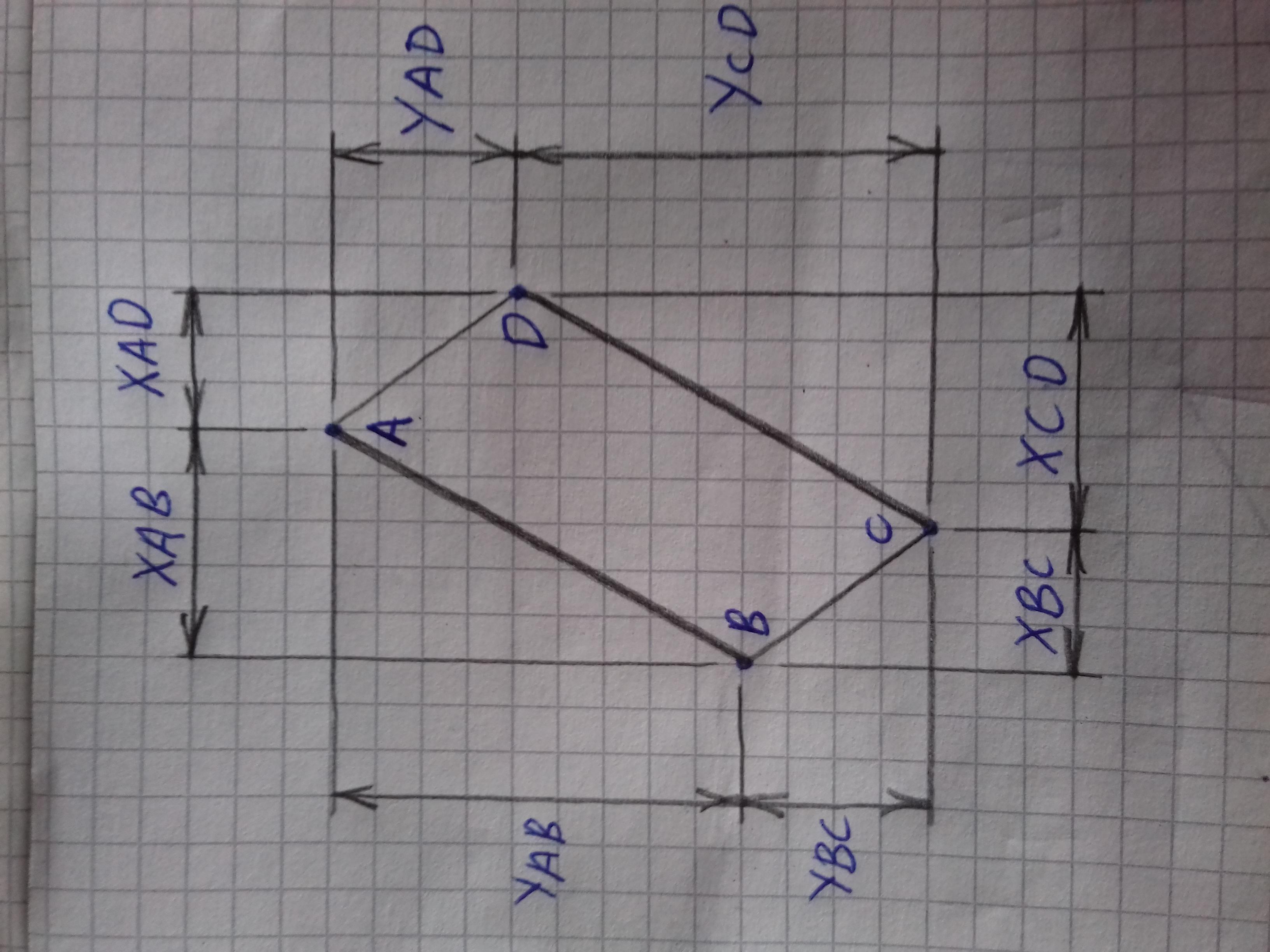
Доведіть що відрізки BC i AD, зображені на рисунку, рівні, якщо AB=CD, AB||CD
Ответы
Відповідь:
Відрізки BC i AD рівні, та параллельні BС = АD, ВС || АD.
Пояснення:
Якщо два відрізки AB та CD параллельні ( AB || CD ), то кути нахилу ціх двох відрізків відносно осі ОХ рівні. У випадку якщо ці два відрізки AB та CD мають однакову довжину ( AB || CD ), то різниця координат Х та У між крапками А-В та C-D рівні ( ХАВ = ХCD, УАВ = УCD ).
Доведемо, що різниця координат Х та У між крапками В-С та А-D рівні ( ХВС = ХАD, УВС = УАD ).
1) ХВС = ХАВ + ХАD - ХСD
Як показано вище ХАВ = ХCD, відповідно отримуємо ХВС = ХАD ( ХАВ та ХCD віднімаються, оскільки вони в рівнянні мають різні знаки ).
1) УВС = УАВ + УАD - УСD
Як показано вище УАВ = УCD, відповідно отримуємо УВС = УАD ( УАВ та УCD віднімаються, оскільки вони в рівнянні мають різні знаки ).
Якщо два відрізки BС та АD мають однакові різниці координат Х та У між крапками В-С та А-D ( ХВС = ХАD, УВС = УАD ), то ці два відрізки рівні ( мають однакову довжину ), та мають однакові кути нахилу відносно осі ОХ.
Відповідно відрізки BC i AD рівні, та параллельні BС = АD, ВС || АD.