помогите пожалуйста
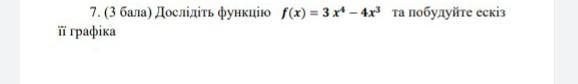
Ответы
f(x)=3x⁴-4x³- исследовать. построить эскиз графика
данная функция определена и дифференцируема на D(f)=R
она не является четной, т.к.
f(-x)=3*(-x)⁴-4*(-x)³=3x⁴+4x³≠f(x) ; не является нечетной, т.к. f(-x)≠-f(x)
f'(x)=12x³-12x²
12x³-12x²=0;
12x²*(х-1)=0
х=0
х=1
исследуем знак производной при переходе через критические точки.
для чего решим неравенство f'(x)<0 методом интервалов
___0______1_____
- - +
функция возрастает на промежутке [1;+∞)
и убывает на промежутке (-∞;0]
точка минимума х=1; минимум у(1)=3-4=-1
нули функции 3х⁴-4х³=0
х³*(3х-4)=0
х=0; х=
______0__________
+ - +
применяя метод интервалов, получаем промежутки знакопостоянства: у>0 при х∈(-∞;0)∪(;+∞); у<0 при х∈ (0;
)
найдем вторую производную
f''(x)=(12x³-12x²)'=36x²-24x
36x²-24x=0
12x*(3x-2)=0
3x-2=0
x=2/3
x=0
_____0_______2/3_______
+ - +
х=0 и х=2/3- точки перегиба. т.к. график на промежутках (-∞;0) ; (2/3;+∞) выпуклый вниз, а при х∈(0;2/3) вверх.
