Question

Четвертый вопрос и пятый помогите​

Answer 1

Ответ:

4. Радиус вписанной окружности равен 4 см.

5. Доказано, что ВМ = р - полупериметру.

Объяснение:

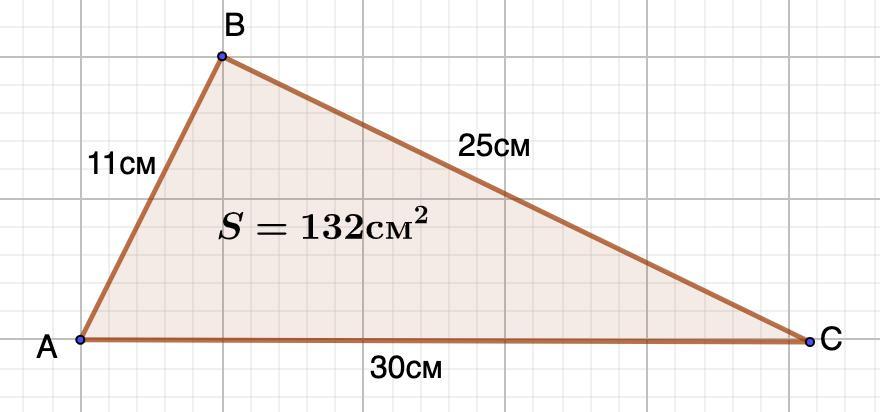
4. Найти радиус вписанной окружности в треугольник АВС.

5. Доказать, что отрезок ВМ равен полупериметру треугольника АВС.

4. Дано: ΔАВС;

S(ABC) = 132 см²;

АВ = 11 см; ВС = 25 см; АС = 30 см.

Найти: r - радиус вписанной окружности.

Решение:

Радиус вписанной окружности найдем по формуле:

$\displaystyle r=\frac{2S}{a+b+c}$ , где a, b, c - стороны треугольника, S - его площадь.

Подставим данные значения:

$\displaystyle r=\frac{2\cdot132}{11+25+30}=4\;_{(CM)}$

Радиус вписанной окружности равен 4 см.

5. Дано: ΔАВС.

Окр.О - вневписанная;

М - точка касания.

Доказать: ВМ = р, где р - полупериметр.

Доказательство:

• Отрезки касательных, проведенных из одной точки, равны.

⇒ МА = АЕ; ЕС = СК; ВМ = ВК.

• Периметр - сумма длин всех сторон треугольника.

Р = АВ + ВС + АС

или Р = АВ + ВС + (АЕ + ЕС)

Так как МА = АЕ; ЕС = СК

⇒ Р = АВ + ВС + (МА + СК) = (АВ + МА) + (ВС + СК) = ВМ + ВК.

Так как ВМ = ВК, то

ВМ = ВК = Р : 2 = р

Доказано, что ВМ = р - полупериметру.