Предмет: Алгебра,
автор: maximmogilev
Нужно сделать 4-5 задание. 100 баллов даю, срочно, в течении 10 минут
Приложения:
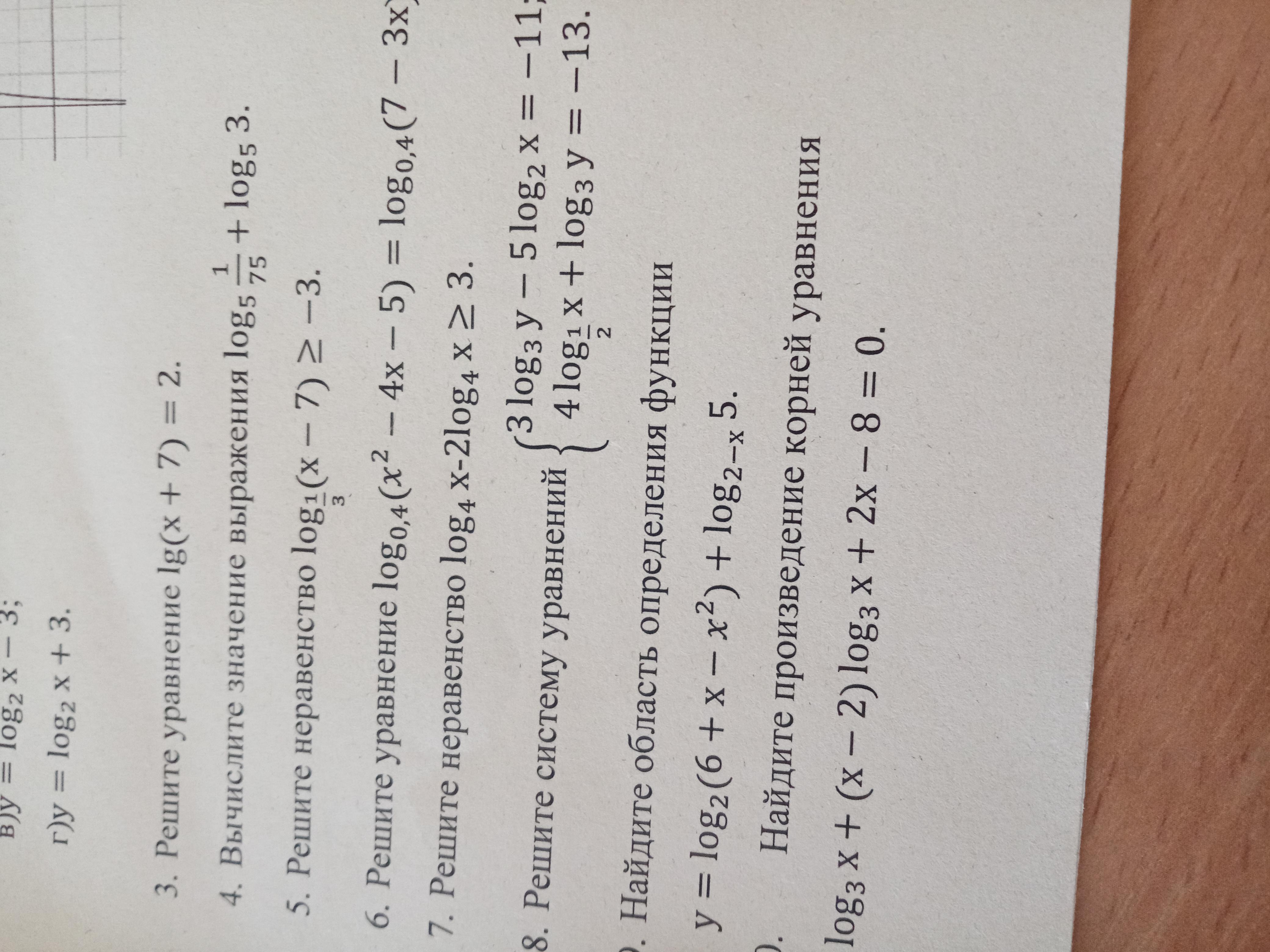
Ответы
Автор ответа:
1
Решение.
Применили свойства логарифмов .
Так как функция убывающая, то при сравнении аргументов знак ставим противоположный:
Учитывая ОДЗ x>7 , получим ответ:
Похожие вопросы
Предмет: Русский язык,
автор: aidaog
Предмет: Другие предметы,
автор: Аноним
Предмет: Русский язык,
автор: ТомирисКазиева
Предмет: Математика,
автор: pykharevaviktoria54
Предмет: Математика,
автор: Аноним