Question

Помогите пожалуйста !!!!!

Answer 1

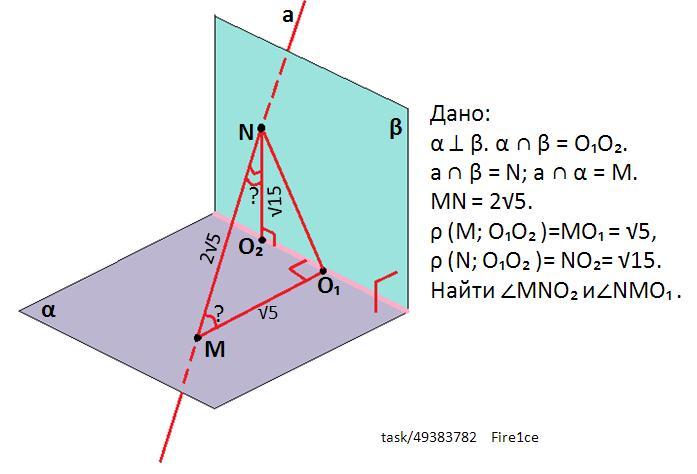
Прямая а пересекает перпендикулярные друг другу плоскости в точках М и N. Расстояния от этих точек до линии пересечений плоскостей: М0₁ = √5 и NО₂ = √15, где О₁ и О₂ - точки, лежащие на линии пересечения плоскостей. Длина отрезка МN равна 2√5. Найдите углы, которые отрезок MN образуют с данными плоскостями.

Ответ:

30° и 60°.

Объяснение:

• Рассмотрим ΔNMО₂.

NО₂⊥О₁О₂ так как расстояние от точки до прямой - перпендикуляр, опущенный с этой точки на прямую.

α ⊥ β, MО₂ лежит в плоскости α, поэтому MО₂⊥ β (По свойству перпендикулярных плоскостей: если прямая лежит в одной из двух взаимно перпендикулярных плоскостей и перпендикулярна линии их пересечения, то эта прямая перпендикулярна второй плоскости).

Если MО₂⊥ β, NО₂ лежит в плоскости β, то MО₂⊥NО₂.

MО₂⊥NО₂. -> ΔNMО₂ - прямоугольный. NО₂ = √15, MN=2√5.

$\LARGE \boldsymbol {} \cos \angle{MNO_2} =\frac{NO_2}{MN} =\frac{\sqrt{15} }{2\sqrt{5} } =\frac{\sqrt{3} }{2} \\\\ \boxed{\angle{MNO_2}=30\°}$

• По аналогии рассмотрим ΔMNО₁.

М0₁⊥О₁О₂ так как расстояние от точки до прямой - перпендикуляр, опущенный с этой точки на прямую.

α ⊥ β, N0₁ лежит в плоскости β, поэтому N0₁⊥ α (По свойству перпендикулярных плоскостей).

Если N0₁⊥ α, М0₁ лежит в плоскости α, то MО₁⊥NО₁.

MО₁ ⊥NО₁ -> ΔMNО₁ - прямоугольный. MN=2√5, М0₁ = √5 .

$\LARGE \boldsymbol {} \cos \angle{NMO_1} =\frac{MO_1}{MN} =\frac{\sqrt{5} }{2\sqrt{5} } =\frac{1 }{2} \\\\ \boxed{\angle{NMO_1}=60\°}$