Задание приложено...
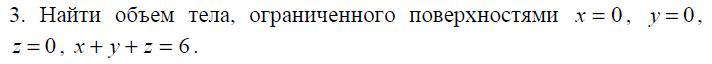
Ответы
Ответ:
кубических единиц
Примечание:
- объем тела ограниченного областью
.
Проектировать тело будем на плоскость , поэтому сведем тройной интеграл к повторному следующим образом:
Распишем приведение двойного интеграла к повторному:
Для вычисления двойного интеграла сведем его к повторному интегралу. Будем интегрировать по x, поэтому приведения в общем
виде к повторному интегралу двойного по области будет в виде:
При этом функции - функции ограничивающие область
снизу и сверху соответственно.
Таким образом тройной интеграл расписывается следующим образом:
То есть:
Объяснение:
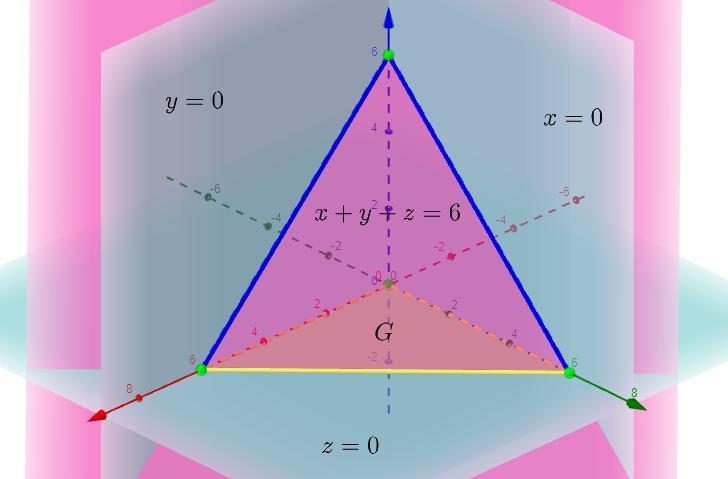
Область ограниченна поверхностями :
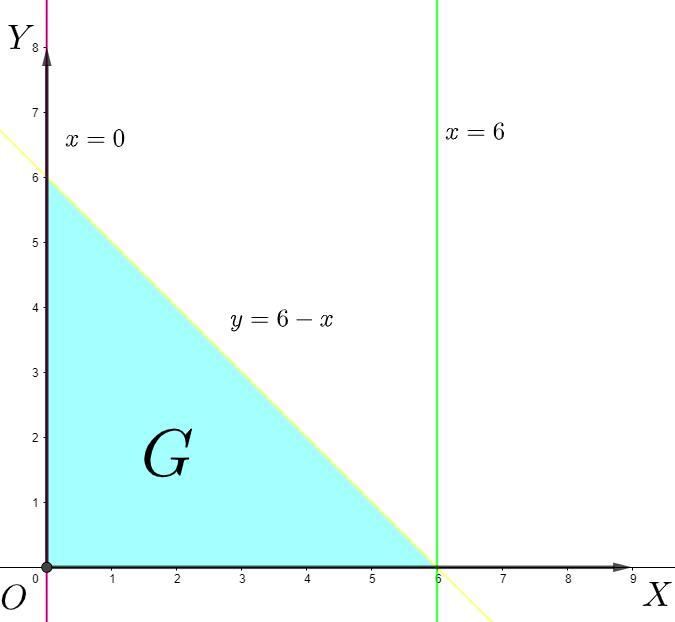
Область
Снизу область ограниченна функцией , а сверху функцией
Пересечения плоскостей
Границы интегрирования: от 0 до 6
------------------------------------------------------------------
кубических единиц.