Question

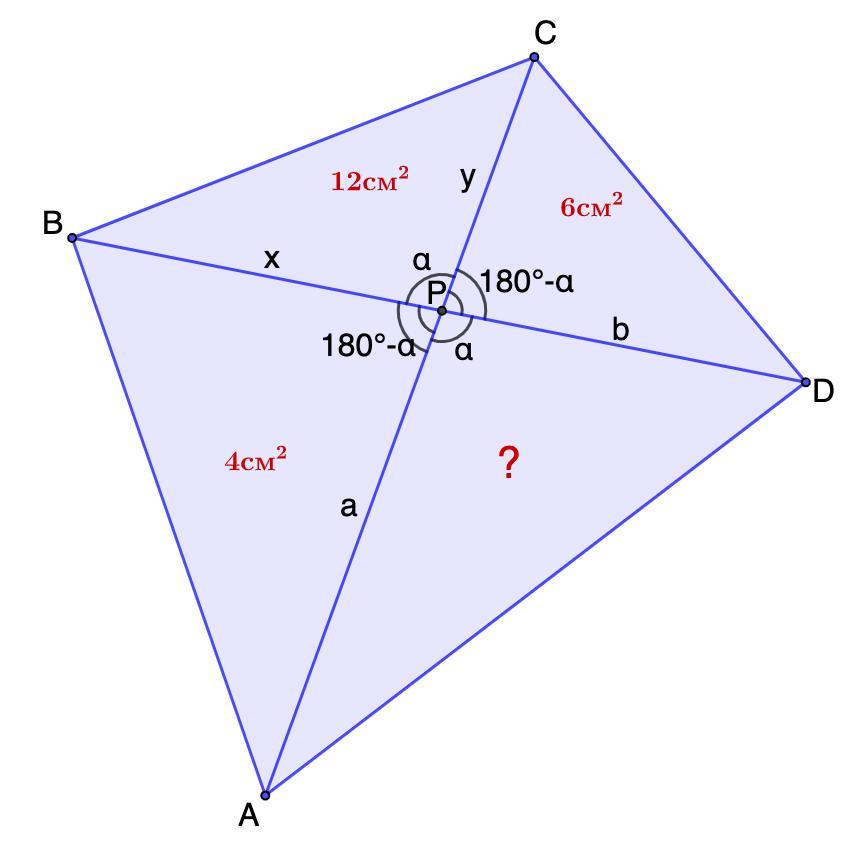
Диагонали четырехугольника ABCD пересекаются в точке P. Найти площадь треугольника АDP, если S ∆ABP = 4 см², S ∆BCP = 12 см², S ∆CDP = 6 см².​​

Answer 1

Ответ:

Площадь треугольника АDP равна 2 см².

Объяснение:

Диагонали четырехугольника ABCD пересекаются в точке P. Найти площадь треугольника АDP, если S ∆ABP = 4 см², S ∆BCP = 12 см², S ∆CDP = 6 см².​​

Дано: ABCD - четырехугольник;

AC ∩ BD = P;

S ∆ABP = 4 см², S ∆BCP = 12 см², S ∆CDP = 6 см².​​

Найти: S ∆АРD.

Решение:

Введем обозначения:

РВ = х; РС = у; АР = а; PD = b.

Теперь разберемся с углами:

Пусть ∠ВРС = α

• Вертикальные углы равны.

⇒ ∠APD = α

• Сумма смежных углов равна 180°.

⇒ ∠ВРА = 180° - α; ∠CPD = 180° - α.

• Синусы смежных углов равны.

⇒ sin α = sin (180° - α)

Также вспомним формулу площади треугольника:

$\displaystyle \boxed { S=\frac{1}{2}ab\cdot{sin\alpha } }$, где a и b - стороны треугольника, α - угол между ними.

1. S ∆BCP = 12 см²

$\displaystyle 12=\frac{1}{2}xy\;sin\alpha \\ \\\boxed {24=xy\;sin\alpha }$

2.  S ∆ABP = 4 см²

$\displaystyle 4=\frac{1}{2}xa\;sin\alpha \\\\xa\;sin\alpha =8\\\\\boxed {a=\frac{8}{x\;sin\alpha } }$

3. S ∆CDP = 6 см².​​

$\displaystyle 6=\frac{1}{2}yb\;sin\alpha \\ \\yb\;sin\alpha =12\\\\\boxed {b=\frac{12}{y\;sin\alpha } }$

4. S ΔAPD = ?

$\displaystyle S(APD) = \frac{1}{2}ab\;sin\alpha$

Подставим значения a и b из п.2 и п.3:

$\displaystyle S(APD)=\frac{1}{2}\cdot\frac{8}{x\;sin\alpha }\cdot\frac{12}{y\;sin\alpha } \cdot{sin\alpha }=\\\\=\frac{48}{\boxed {xy\;sin\alpha} } =\frac{48}{24}=2\;_{(CM^2)}$

Площадь треугольника АDP равна 2 см².