Предмет: Алгебра,
автор: vrusyt22
Помогите пожалуйста
{x^2-3x+9>0
{x^2<36
-
Приложения:
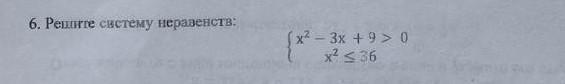
Ответы
Автор ответа:
1
Решение.
Так как D<0 и a=1>0 , то квадратный трёхчлен при любых значениях переменной х принимает положительные значения .
Ответ: .
vrusyt22:
Спасибо,но я не понимаю что с сверху красное
это твой телефон не распознаёт редактор формул , зайди на сайт не с телефона
Похожие вопросы
Предмет: Английский язык,
автор: ANNAANNAA11Aannana
Предмет: Окружающий мир,
автор: Вера234673
Предмет: Русский язык,
автор: aksyirekkuramys
Предмет: Математика,
автор: ljolik73