Question

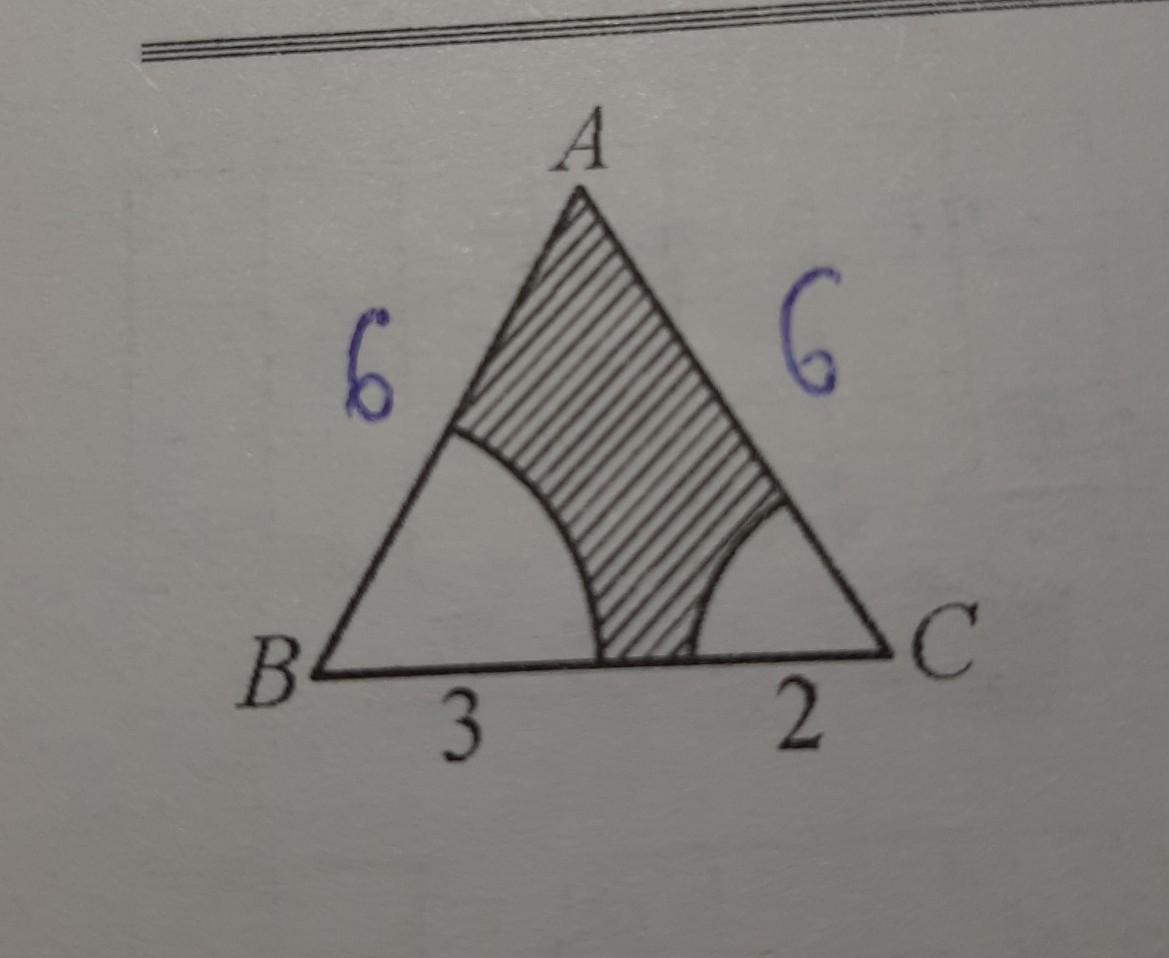
Найдите площадь заштрихованной фигуры, если AB=AC=BC=6см​

Answer 1

Ответ:

Треугольник равносторонний, значит все углы 60°.

Формула площади равностороннего треугольника:

$\displaystyle S = \frac{ {a}^{2} \sqrt{3} }{4}$

$S_{ \triangle ABC} = \frac{ {6}^{2} \sqrt{3} }{4} = \frac{36 \sqrt{3} }{4} = 9 \sqrt{3}$

В треугольник две дуги, которые можно дочертить до круга.

Часть круга, заключённая между радиусами и дугой, называется сектором круга.

Площадь сектора круга:

$S = \frac{ {r}^{2} \alpha }{2}$

α – центральный угол сектора в радианах.

Чтобы перевести угол в градусах в радианы, надо умножить угол на π/180°.

α=60°

${60}^{ \circ} \times \frac{\pi}{ {180}^{\circ} } = \frac{\pi}{3}$

Найдем площадь сектора круга из вершины B.

$S_{1} = \frac{ {3}^{2} \times \frac{\pi}{3} }{2} = \frac{9 \times \frac{\pi}{3} }{2} = \frac{3\pi}{2}$

Второго сектора из вершины C:

$S_{2}= \frac{ {2}^{2} \times \frac{\pi}{3} }{2} = \frac{4 \times \frac{\pi}{3} }{2} = \frac{2\pi}{3}$

Площадь закрашенной части:

$S=S_{\triangle ABC} - S_{1} - S_{2}$

$\displaystyle S = 9 \sqrt{3} - \frac{3\pi}{2} - \frac{2\pi}{3} = 9 \sqrt{3} - \frac{9\pi - 4\pi}{6} = 9 \sqrt{3} - \frac{5\pi}{6}$

Ответ: S=9√3-(5π)/6 см².