Предмет: Геометрия,
автор: shbdj
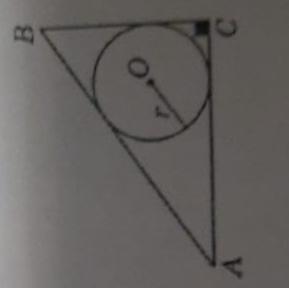
В прямоугольный треугольник, гипотенуза которого равна 13 сантиметров, а один из катетов равен 5 сантиметров, вписана окружность. Найдите радиус окружности.
Пожалуйста, решите эту задачу. Только прошу не по теореме Пифагора, и не системой уравнения. И желательно вообще не решать через простое уравнение. (На фото чертёж)
Приложения:
Ответы
Автор ответа:
1
Ответ:
БЕЗ ТЕОРЕМЫ ПИФАГОРА НИКАК, ТЕБЕ НЕОБХОДИМА 3 СТОРОНА
Кхм... Гипотенуза=13
1 катет=5
по Т. Пифагора, 2 катет=12
Площадь треугольника равна a*b=
*12*5=30
Также площадь находится по формуле Pr (эта формула применяется если в многоугольник можно вписать окружность, а у нас она вписана в треугольник)
Получаем 30=Pr; P=13+12+5=30
30=*30*r
Отсюда r=2
Ответ:Радиус равен 2
shbdj:
Спасибо за решение, хотя бы что-то сдам учительнице, а не пустую тетрадь ;)
Ахахах, учи геометрию! а то потом сложно будет
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: Solnce2008
Предмет: Русский язык,
автор: mezentzevavale
Предмет: Математика,
автор: gametv70167830