Question

Реши задачу.


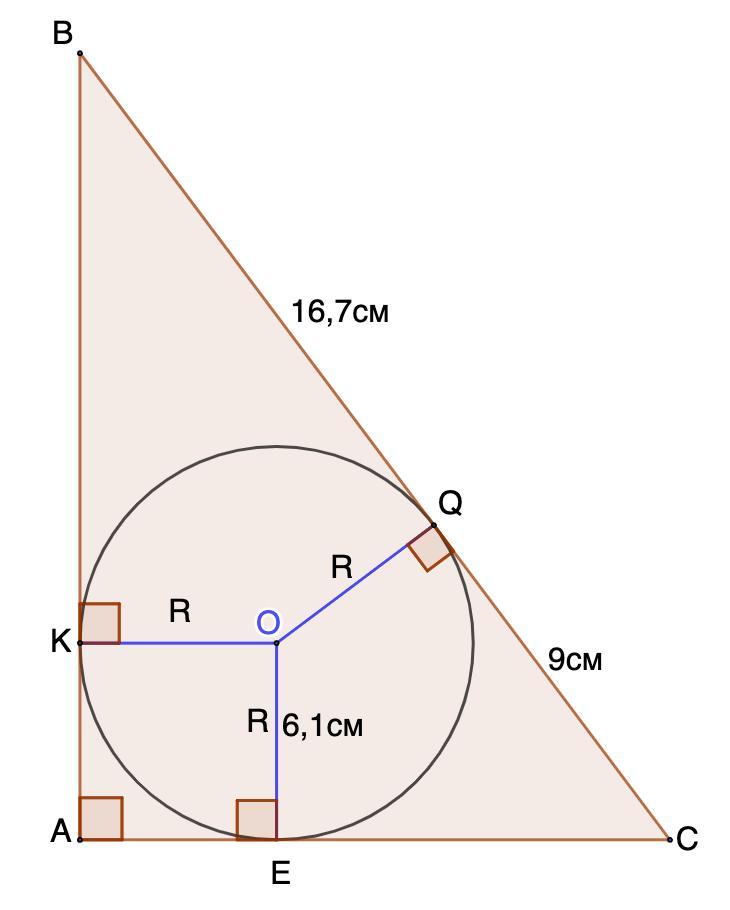
Окружность с радиусом 6,1 6,1 см вписана в прямоугольный треугольник. Найди периметр треугольника, если точка касания Q Q делит гипотенузу на отрезки, равные 16,716,7 и 9 9 см. Вырази ответ в см.


Запиши ответ числом.

Answer 1

Ответ:

Периметр треугольника равен 63,6 см.

Объяснение:

Окружность с радиусом  6,1 см вписана в прямоугольный треугольник. Найди периметр треугольника, если точка касания  Q  делит гипотенузу на отрезки, равные  16,7 см и  9 см.

Дано: ΔАВС - прямоугольный.

Окр.О,R - вписана в ΔАВС.

R = 6,1 см;

Q ∈ BC - точка касания;

BQ = 16,7 см; QС = 9 см.

Найти: Р (АВС)

Решение:

1. Рассмотрим АКОЕ.

∠А = 90° (условие)

• Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ ∠ АКО = 90°; ∠ОЕА = 90°.

⇒ АКОЕ - прямоугольник.

• Противоположные стороны прямоугольника равны.

⇒ АК = ОЕ = R = 6,1 см; ОК = АЕ = R = 6,1 см;

2.

• Отрезки касательных, проведенных из одной точки, равны.

⇒ BK = BQ = 16,7 см; CQ = CE = 9 см.

3.

• Периметр - сумма длин всех сторон треугольника.

Р(АВС) = АВ + ВС + АС.

или

Р(АВС) = АК + КВ + BQ + QC + CE + EA =

= 6,1 + 16,7 + 16,7 + 9 + 9 + 6,1 = 63,6 (см)

Периметр треугольника равен 63,6 см.

#SPJ1