Предмет: Алгебра,
автор: narasikanura
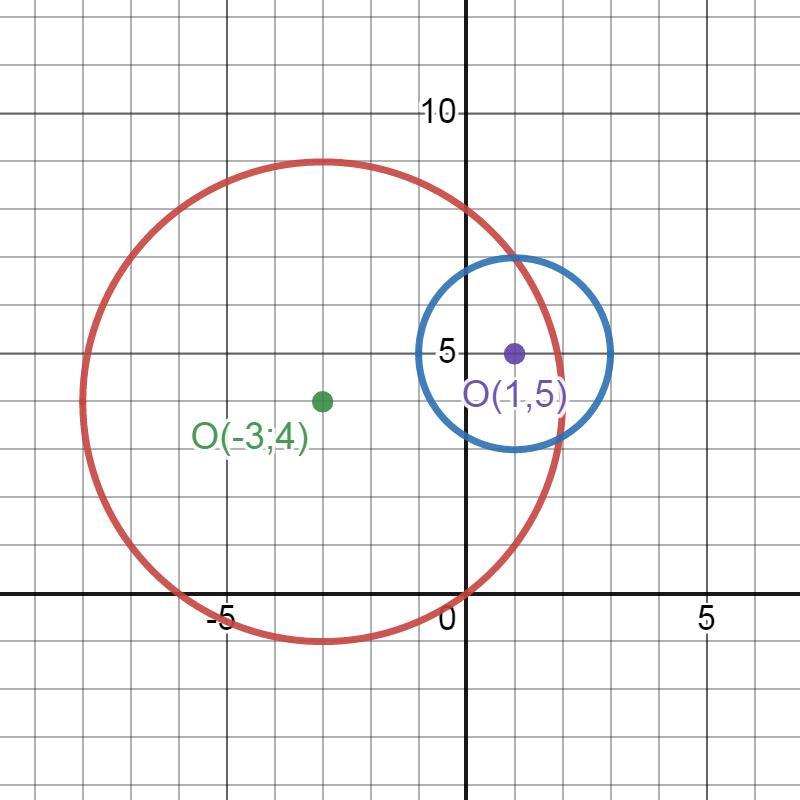
3. Выполните построение , выясните взаимное расположение двух окружностей , заданных уравениями: (x+3)^2+(y-4)^2=25и(x-1)^2+(y-5)^2=4
Ответы
Автор ответа:
1
Уравнение окружности имеет вид:
Где (х₀; у₀) - координаты центра окружности, а R - радиус окружности.
(-3; 4) - центр окружности, R = 5 - радиус окружности
(1; 5) - центр окружности, R = 2 - радиус окружности
На рисунке видно, что окружности пересекаются
Приложения:

Автор ответа:
0
Объяснение:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: тима156
Предмет: Русский язык,
автор: bav1911
Предмет: Қазақ тiлi,
автор: перйзат
Предмет: Математика,
автор: tsukalov09
Предмет: Русский язык,
автор: meslorama12