Предмет: Алгебра,
автор: vikahrapolovic
Помогите пожалуйста!!!!!!@
Алгебра 10 класс!!!!!!!!!
Приложения:
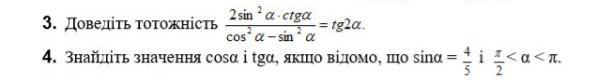
Ответы
Автор ответа:
4
1. Доказать тождество (2sin^2 a * ctg a)/(cos^2 a-sin^2 a)=tg2a.
2. Найти cos(a) и tg(a) если sin(a) = 4/5 и π/2<а<π.
Ответ:
1. Тождество доказано (решение ниже).
2. cos a = (-3/5) и tg a = (-4/3).
Формулы:
Объяснение:
1. Доказать тождество (2sin^2 a * ctg a)/(cos^2 a-sin^2 a)=tg2a.
Начнём преобразование левой части уравнения применяя вышеуказанные формулы и будем продолжать до тех пор, пока не дойдём до tg 2a.
Тождество доказано.
2. Найти cos(a) и tg(a) если sin(a) = 4/5 и π/2<а<π.
π/2<а<π, поэтому а лежит во второй четверти. Во II четверти косинус отрицательный.
Найдём cos(a) используя основное тригонометрическое тождество:
Найдём tg a = (sin a)/(cos a):
Во II четверти тангенс отрицательный, соответственно:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Русский язык,
автор: Nadir12
Предмет: Русский язык,
автор: beldem
Предмет: Биология,
автор: popylovskiks
Предмет: Обществознание,
автор: alexandrpupkin228