Question

допоможіть, будь ласка, терміново треба
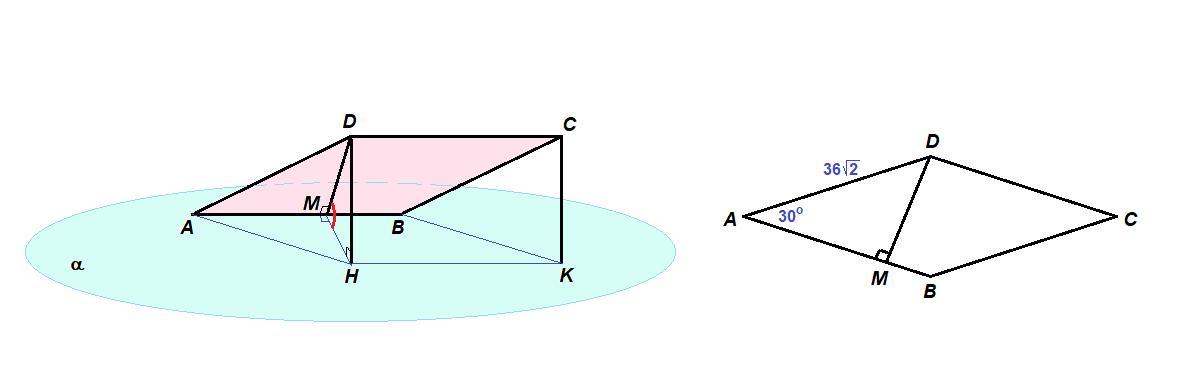
Через сторону АВ ромба АВСD проведено площину а, що утворює з площиною ромба кут 45°. Обчисліть відстань від прямoї CD до площини а, якщо гострий кут ромба дорівнює 30° і АВ=36√2
​

Answer 1

Ответ:

Расстояние от прямой CD до плоскости α равно 18.

Объяснение:

Проведем DH - перпендикуляр к плоскости α из точки D.

Проведем DM⊥АВ, МН - проекция DM на плоскость α, тогда МН⊥АВ по теореме, обратной теореме о трех перпендикулярах.

DM⊥АВ и МН⊥АВ, значит ∠DMH = 45° - угол между плоскостью α и плоскостью ромба.

CD║АВ, АВ ⊂ α, значит CD║α.

• Расстояние от прямой, параллельной плоскости, до этой плоскости - это длина перпендикуляра, проведенного из любой точки прямой к плоскости.

DH - искомое расстояние.

ΔADM: ∠AMD = 90°, DM = 0,5·AD = 0,5 · 36√2 = 18√2 по свойству катета, лежащего против угла в 30°.

ΔDMH: ∠DHM = 90°,  ∠DMH = 45°

 $\sin\angle DMH=\dfrac{DH}{DM}$

$\dfrac{\sqrt{2}}{2}=\dfrac{DH}{18\sqrt{2}}$

$DH=\dfrac{18\sqrt{2}\cdot \sqrt{2}}{2}=9\cdot 2=18$