Question

помогите пожалуйста
​

Answer 1

Ответ:

$f(x) = \frac{ {x}^{4} }{2} - 2x + \frac{3}{2}$

Отрезок [-1;2]

Сначала проверим эти точки, потому что они сами входят в этот промежуток. (Если попроще, если квадратные скобки, то проверяем; ну а если круглые скобки, то это числа не входят в промежуток, поэтому их не проверяют. В нашем случае квадратные скобки)

$f( - 1) = \frac{ {( - 1)}^{4} }{2} - 2 \times ( - 1) + \frac{3}{2} = \frac{1}{2} + 2 + \frac{3}{2} = 4$

$f(2) = \frac{ {2}^{4} }{2} - 2 \times 2 + \frac{3}{2} = \frac{16}{2} - 4 + \frac{3}{2} = 4 + \frac{3}{2} = 5.5$

Найдем производную:

$f'(x) = 2 {x}^{3} - 2$

Приравняем производную нулю:

$2 {x}^{3} - 2 = 0 \\ {x}^{3} - 1 = 0 \\ {x}^{3} = 1 \\ x = \sqrt[3]{1} \\ x = 1$

1 лежит в промежутке [-1; 2], поэтому проверяем является ли он точкой экстремума.

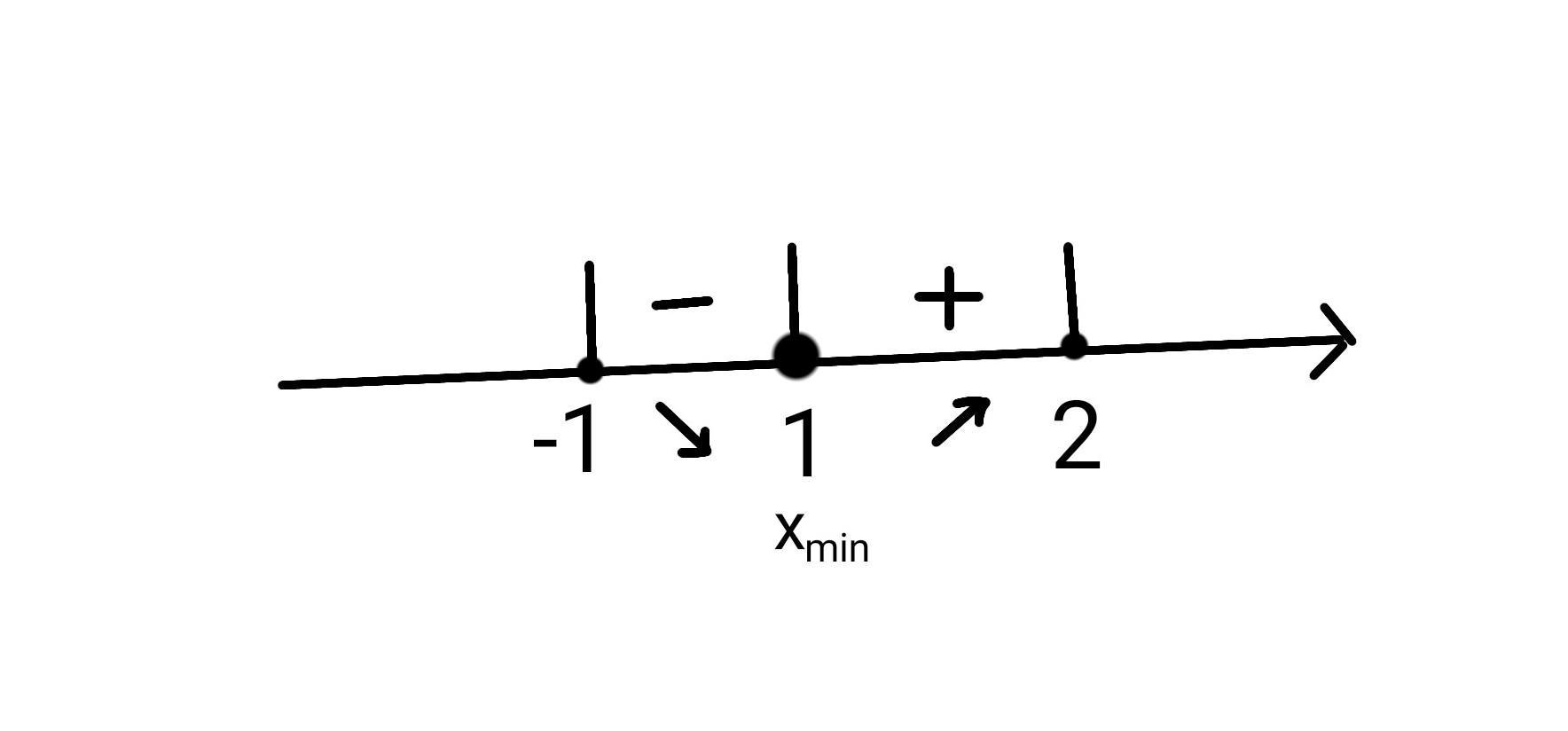
Чертим числовую ось (прикрепил фото).

Проверяем возрастает или убывает функция в промежутке (-1;1), для этого берем любое число между -1 и 1, но не их самих. Для удобства возьмем 0 и подставим в производную.

$f'(0) = 2 \times {0}^{3} - 2 = 0 - 2 = - 2$

Значение отрицательное, значит функция в промежутке (-1;1) убывает. (Для удобства отметим на числовой оси стрелкой вниз, если убывает, и стрелкой вверх, если возрастает)

Теперь проверим промежуток (1;2)

Возьмем число 1,5.

$\displaystyle f'( \frac{3}{2} ) = 2 \times {( \frac{3}{2}) }^{3} - 2 = 2 \times \frac{27}{8} - 2 = \frac{27}{4} - \frac{8}{4} = \frac{19}{4}$

Ответ положительный, значит в промежутке (1;1) функция возрастает (отметим стрелкой).

Если до точки функция убывала, после точки начала возрастать, то это точка минимума.

Если же до точки возрастала и после начала убывать, то это точка максимума.

Точки максимума и минимума – это экстремумы или же экстремальные точки.

У нас убывала и начала возрастать, значит точка 1 – точка минимума.

Теперь проверим значение функции в точке 1.

$f(1) = \frac{ {1}^{4} }{2} - 2 \times 1 + \frac{3}{2} = \frac{1}{2} - 2 + \frac{3}{2} = 2 - 2 = 0$

У нас вышли три значения:

4; 5,5; 0

Наибольшее значение равняется 5,5 в точке x=2.

Наименьшее же равняется 0 в точке x=1.

Ответ: 0