Question

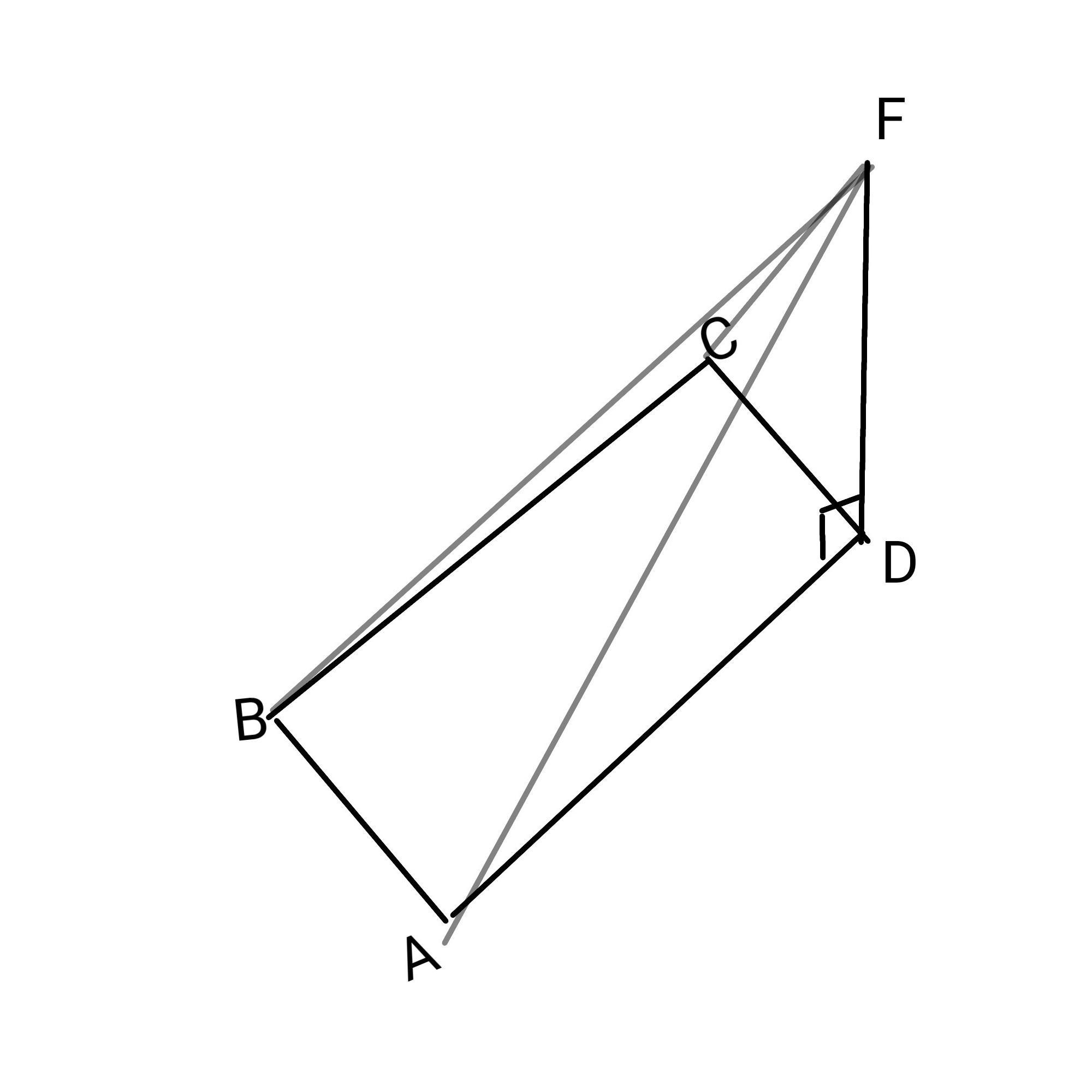
Из вершин D прямоугольника ABCD стороны которого равны AB=9см и BC=8см, восстановлен к плоскости ABCD перпендикуляр DF=12см. Найдите расстояние от точки F до вершин прямоугольника

Answer 1

Ответ:

AD=BC=8; AB=CD=9

Образуются прямоугольные треугольники: ΔAFD; ΔBFD; ΔCFD.

Надо найти AF; BF; CF.

Рассмотрим ΔAFD:

AD=8

DF=12

По теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов.

c²=a²+b²

AF²=AD²+DF²

AF²=8²+12²

AF²=64+144

AF²=208

AF=√208

AF=4√13

Теперь рассмотрим треугольник ΔCFD:

CD=9

По теореме Пифагора:

CF²=CD²+DF²

CF²=9²+12²

CF²=81+144

CF²=225

CF=√225

CF=15

Чтобы найти отрезок BF, сначала нужно найти отрезок BD.

По теореме Пифагора, в треугольнике ABD:

BD²=AB²+AD²

BD²=9²+8²

BD²=81+64

BD²=145

Теперь в треугольнике BFD:

BF²=BD²+DF²

BF²=145+12²

BF²=145+144

BF²=289

BF=√289

BF=17

Ответ: AF=4√13 см; BF=17 см; CF=15 см.