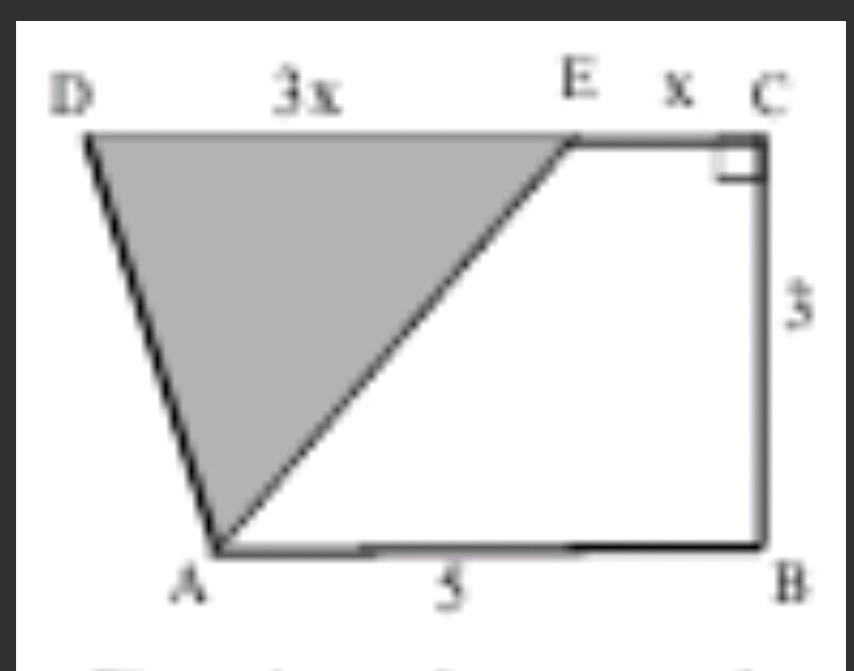
ABCD представляет собой трапецию с EC = x и ED = 3x, BC =3, AB=5. Если площадь ABCD равна 19,5, какова площадь заштрихованной области?
Ответы
Ответ:
Ответ: задача3: 13,5
задача4: 13
задача2: Q
Объяснение: задача 3.
1.площадь квадрата = а², то есть сторона в квадрате, так как площадь равна 1, то сторона равна√1=1
2.проведем ВО - высоту к АД
3.треугольник АВО прямоугольный; ВО = 3 и АО = 2 (1 клетка=1)
площадь АВО= 1/2·АО·ВО= 1/2·2·3= 3
4. Проведем высоту СК к АД
5. треугольник СКД прямоугольный; СК = 3 и КД = 1
площадь СКД= 1/2·СК·КД= 1/2·3·1= 1,5
это формулы площадей треугольников (S=1/2·a·b)
6. площадь ОВСК= 3·3= 9
7.Sавсд= Saво+Scкд+Sовск= 3+1,5+9=13,5
задача 4.
1. Проведем ДО перпендикулярно к АF
Следовательно, ВС параллельно АО и СО параллельно АВ
Следует, что ВС=АО=3
2. ОF= АF-АО=5-3=2
3. ДО параллельно ЕF и ДЕ параллельно ОF
следовательно, ДЕ=ОF=2 и ДО=ЕF=2
4.площадь ОДЕF=ДЕ·ЕF=2·2=4
5. площадь АВСО= АВ·ВС=3·3=9
6. площадь АВСДЕF= площадь АВСО+ площадь ОДЕF= 4+9=13
задача 2.
1. рассмотрим треугольники СЕF и АЕД — они прямоугольные:
СЕ=ЕД и уголСЕF=углуАЕД (как вертикальные углы)
Следовательно, треугольники равны СЕF=АЕД (по катету и прилежащему к нему углу)
2. Sавсд= Sавсе+Sаед
Saвf= Saвсе+Sсеf
то есть Saвf= Saвсе+Saед=Q
Объяснение: