Question

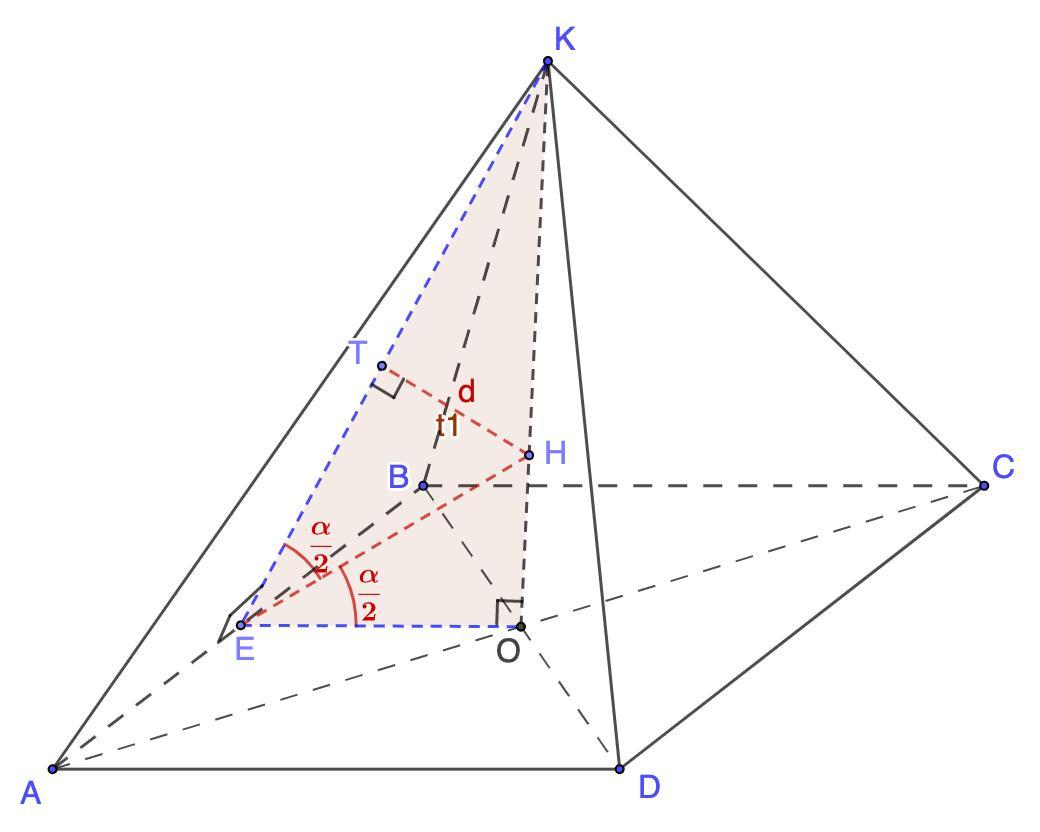
У правильній чотирикутній піраміді кут між апофемою і площиною основи дорівнює а. Бісектриса цього кута перетинає висоту піраміди в точці, яка розміщена на відстані d від апофеми. Знайдіть бічну поверхню піраміди.

Answer 1

Ответ:

Боковая поверхность пирамиды равна $\displaystyle S_{bok}=\frac{4d^2}{tg^2\frac{\alpha }{2}\cdot{cos\;\alpha } }$  ед.²

Объяснение:

В правильной четырехугольной пирамиде угол между апофемой и плоскостью основания равен α. Биссектриса этого угла пересекает высоту пирамиды в точке, которая размещена на расстоянии d от апофемы.  Найдите боковую поверхность пирамиды.

Дано: KABCD - правильная пирамида;

КЕ - апофема;

∠КЕО = α;

ЕН - биссектриса ∠КЕО;

Расстояние от Н до КЕ равно d.

Найти: S бок.

Решение:

• Расстояние от точки до прямой - длина перпендикуляра, опущенного из данной точки на данную прямую.

⇒ НТ ⊥ ЕК; НТ = d.

• Площадь боковой поверхности пирамиды равна половине произведения периметра основания на апофему.

$\displaystyle \boxed { S_{bok}=\frac{1}{2}P_{osn}\cdot{h}}$ , где h - апофема.

• В основании правильной четырехугольной пирамиды лежит квадрат.

⇒ необходимо найти сторону квадрата и апофему.

1. Рассмотрим ΔЕТН и ΔЕНО - прямоугольные.

∠ТЕН = ∠НЕО = α/2 (ЕН - биссектриса)

ЕН - общая.

⇒ ΔЕТН = ΔЕНО (по гипотенузе и острого углу)

• В равных треугольниках против равных углов лежат равные стороны.

⇒ ТН = НО = d

2. Найдем сторону основания.

Рассмотрим ΔЕНО - прямоугольный.

• Тангенс угла - отношение противолежащего катета к гипотенузе.

$\displaystyle tg\;\frac{\alpha }{2}=\frac{HO}{EO} \\\\EO=\frac{HO}{tg\;\frac{\alpha }{2} } =\frac{d}{tg\;\frac{\alpha }{2} }$

⇒  $\displaystyle AD = 2EO=\frac{2d}{tg\;\frac{\alpha }{2} }$

3. Найдем апофему.

Рассмотрим ΔЕКО - прямоугольный.

• Косинус угла - отношение прилежащего катета к гипотенузе.

$\displaystyle cos\;\alpha =\frac{EO}{EK}\\ \\EK=\frac{EO}{cos\;\alpha } =\frac{d}{tg\;\frac{\alpha }{2} \cdot{cos\;\alpha }}$

4. Теперь можем найти S бок.

$\displaystyle P_{osn}=AD\cdot4=\frac{8d}{tg\;\frac{\alpha }{2} }$

$\displaystyle S_{bok}=\frac{1}{2}\cdot\frac{8d}{tg\;\frac{\alpha }{2} }\cdot\frac{d}{tg\;\frac{\alpha }{2}\cdot{cos\;\alpha } } =\frac{4d^2}{tg^2\frac{\alpha }{2}\cdot{cos\;\alpha } }$

Боковая поверхность пирамиды равна $\displaystyle S_{bok}=\frac{4d^2}{tg^2\frac{\alpha }{2}\cdot{cos\;\alpha } }$  ед.²

#SPJ1