Question

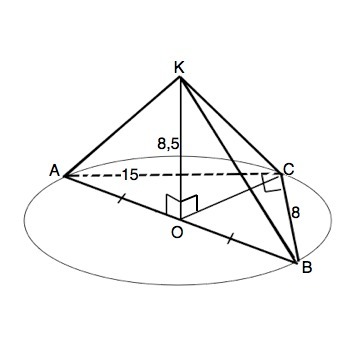
Через середину гипотенузы прямоугольного треугольника ABC проведен к его плоскости перпендикуляр КО равный 8.5 см BC=8cm AC=15cm. Вычислите углы между плоскостью треугольника и наклонными КА КВ КС

Answer 1

По т.Пифагора гипотенуза ∆ АВС

АВ=√(AC²+BC²)=√(225+64)=17 см.

Тогда АО=ОВ=8,5 см, 

СО - медиана ∆ АВС, и  равен половине гипотенузы по свойству медианы прямоугольного треугольника. СО= 8,5 см 

 КО ⊥ плоскости ∆ АВС, проекции наклонных АК, ВК, СК равны, ⇒  равны и сами  эти наклонные. 

В прямоугольных ∆ АКО, ∆ ВКО и Δ СКО катеты равны, ⇒ эти треугольники равные равнобедренные. 

Острые углы равнобедренных прямоугольных треугольников равны 45° , ⇒ 

углы между плоскостью ∆ АВС и наклонными АК, ВК и СК равны 45°.