Question

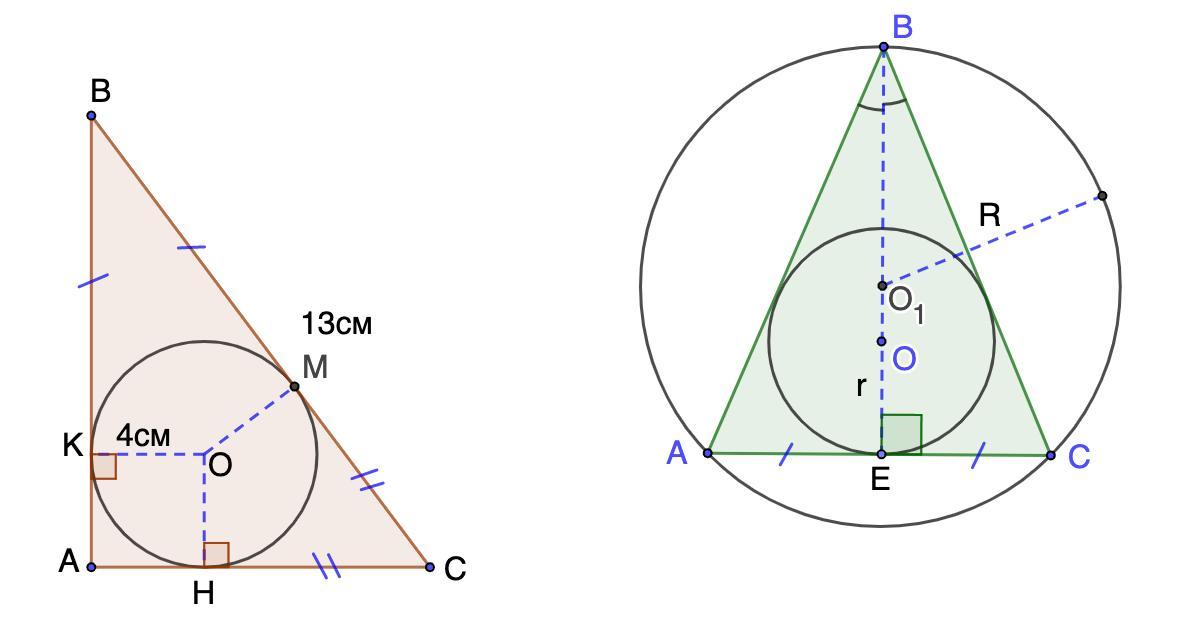
6. в прямоугольный треугольник вписана окружность радиуса 4 см гипотенуза треугольника равна 13 см найдите пример и площадь этого треугольника
7)в равнобедренном треугольнике основание равно 18см а высота приведенная к очнованию
равна 12 см найдите радиус вписанной и описанной окружностей

Answer 1

Ответ:

6. Периметр треугольника равен 34 см.

Площадь треугольника равна 68 см².

7. Радиус окружности, вписанной в треугольник равен 4,5 см.

Радиус окружности, описанной около треугольника равен 9,375 см.

Объяснение:

6. В прямоугольный треугольник вписана окружность радиуса 4 см. Гипотенуза треугольника равна 13 см. Найдите периметр и площадь этого треугольника.

7. В равнобедренном треугольнике основание равно 18 см, а высота приведенная к основанию равна 12 см. Найдите радиусы вписанной и описанной окружностей.

6.

Дано: ΔАВС - прямоугольный;

r = 4 см - радиус вписанной окружности;

ВС = 13 - гипотенуза;

Найти: Р(АВС); S(АВС).

Решение:

1. Рассмотрим АКОН.

• Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ ОК ⊥ АВ; ОН ⊥ АС.

∠А = 90° (условие)

⇒ АКОН - прямоугольник.

• Противоположные стороны прямоугольника равны.

⇒ КО = ОН = ОН = АК = 4 см.

⇒ АКОН - квадрат.

2. Рассмотрим ΔАВС - прямоугольный.

• Отрезки касательных, проведенных из одной точки, равны.

⇒ ВК = ВМ; СН = СМ.

ВС = ВМ + МС = 13 см

или

ВК + СН = 13 см.

• Периметр - сумма длин всех сторон.

Р(АВС) = АВ + ВС + АС = АК + ВК + ВС + АН + СН =

= 4 + 13 + 13 + 4 = 34 (см)

Периметр треугольника равен 34 см.

Найдем площадь.

• Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.

S(АВС) = 0,5 · 34 · 4 = 68 (см²)

Площадь треугольника равна 68 см².

7.

Дано: ΔАВС - равнобедренный;

Окр.О,r - вписанная в ΔАВС;

Окр.О₁,R - описана около ΔАВС;

АС = 18 см - основание;

ВЕ = 12 см - высота.

Найти: r; R.

Решение:

1. Рассмотрим ΔАВС - равнобедренный.

• В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.

⇒ АЕ = ЕС = 18 : 2 = 9 (см)

• Центр вписанной окружности лежит на биссектрисе угла.

⇒ О ∈ ВЕ.

2. Рассмотрим ΔЕВС - прямоугольный.

По теореме Пифагора найдем ВС:

ВС² = ЕС² + ВЕ² = 81 + 144 = 225

ВС = √225 = 15 (см)

3. Найдем r - радиус вписанной окружности.

$\displaystyle r=\frac{S}{p}$ , где S - площадь треугольника, р - полупериметр.

• Периметр - сумма длин всех сторон.

⇒ р = (АВ + ВС + АС) : 2 = (15 + 15 + 18) : 2 = 24 (см)

• Площадь треугольника равна половине произведения высоты на сторону, к которой проведена высота.

S = 0,5 · AC · ВЕ = 0,5 · 18 · 12 = 108 (см²)

r = 108 : 24 = 4,5 (см)

Радиус окружности, вписанной в треугольник равен 4,5 см.

4. Найдем R - радиус описанной окружности.

$\displaystyle R=\frac{abc}{4S}$ , где a, b, c - стороны треугольника, S - площадь.

$\displaystyle R = \frac{18\cdot15\cdot15}{4\cdot108} =9,375\;_{(CM)}$

Радиус окружности, описанной около треугольника равен 9,375 см.