Question

Равнобедренный треугольник со сторонами 10, 10 и 12 вращается вокруг медианы, проведенной к основанию. Найдите площадь поверхности полученного тела.

Answer 1

Ответ:

S = 96π см²

Объяснение:

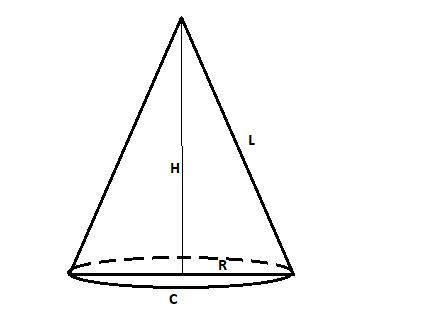
Это тело - конус. Его радиус равен R = 12/2 = 6 см, а образующая равна боковой стороне треугольника L = 10 см.

Смотрите рисунок.

Высоту конуса можно найти из теоремы Пифагора:

H² = L² - R² = 10² - 6² = 100 - 36 = 64

H = 8 см.

Длина окружности основания:

C = 2π*R = 2*6*π = 12π см

Площадь поверхности конуса состоит из основания и боковой части.

Площадь основания:

S(осн) = π*R² = π*6² = 36π см²

Боковую поверхность конуса можно развернуть на плоскости, получится сектор.

Радиус этого сектора равен образующей L = 10 см.

Длина дуги сектора равна длине окружности основания C = 12π см.

Найдем величину угла сектора по формуле длины дуги:

C = π*L*α/180° = 12π

α = 180*C/(π*L) = 180*12π/(π*10) = 18*12 = 216°

Площадь боковой поверхности конуса:

S(бок) = π*L²*α/360° = π*10²*216/360 = 100π*6/10 = 60π см²

Площадь полной поверхности:

S = S(осн) + S(бок) = 36π + 60π = 96π см²