Предмет: Алгебра,
автор: grisenkovalerij80
Допоможіть будь ласка
Приложения:
Ответы
Автор ответа:
1
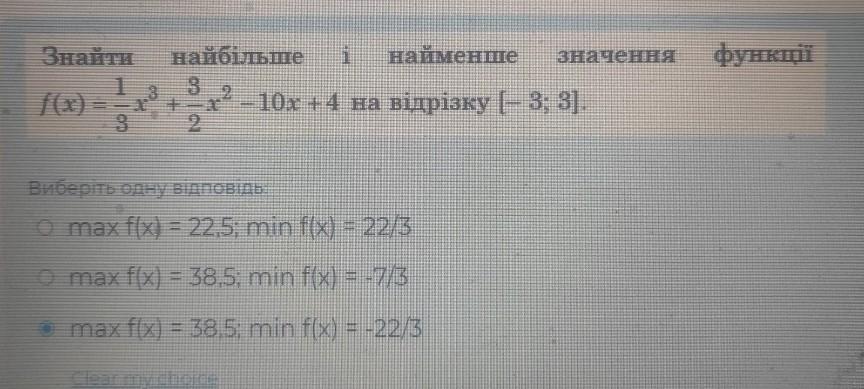
Найти наибольшее и наименьшее значения функции f(x) = (1/3)x^3+(3/2)x^2-10x+4 на промежутке .
Ответ:
max f(x)=38.5; min f(x)=(-22/3).
Объяснение:
Алгоритм нахождения наибольшего и наименьшего значений функции на заданном промежутке:
- Находим критические точки.
- Вычисляем значения функции в критических точках, которые принадлежат заданному промежутку и в крайних точках промежутка.
- Выбираем наибольшее и наименьшее из них.
Найдём производную функции:
Найдём критические точки, которые принадлежат заданному промежутку:
Единственная критическая точка, которая принадлежит промежутку [-3;3] - х=2. Находим значение функции в этой критической точке и крайних точках промежутка, тоесть f(2), f(-3) и f(3).
Среди получившихся значений выбираем наибольшее и наименьшее:
Похожие вопросы
Предмет: Другие предметы,
автор: Полина3339
Предмет: Русский язык,
автор: MaJl4yk2005
Предмет: Английский язык,
автор: verb4
Предмет: Геометрия,
автор: SvyatoslavGorinskiy
Предмет: Математика,
автор: Аноним