Предмет: Алгебра,
автор: minecraft2004one
Помогите пж! Даю 100 баллов!
Приложения:
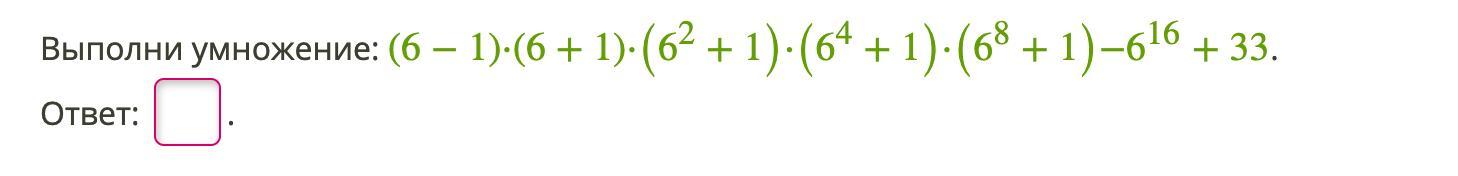

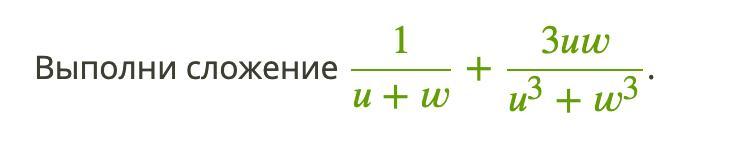
spamgg002:
только ответ нужен?
да
Ответы
Автор ответа:
1
Решение.
1. Применяем последовательно формулу разности квадратов.
2. Применяем свойства степеней .
3. Применяем формулы и
.
Похожие вопросы
Предмет: Русский язык,
автор: Нарине2008
Предмет: Английский язык,
автор: Studentik321
Предмет: Русский язык,
автор: Бибимариям
Предмет: География,
автор: iarinaua
Предмет: Математика,
автор: liliya3299