Question

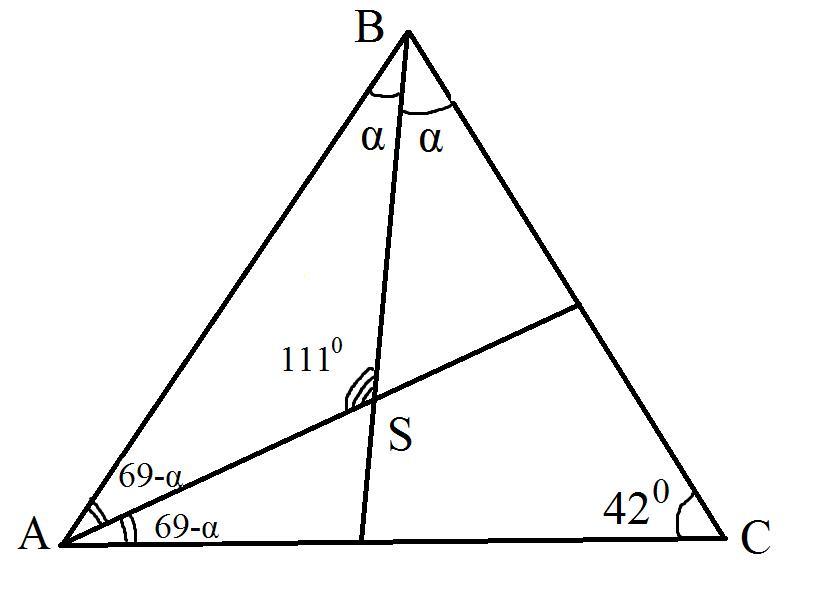
В треугольнике ABC угол C равен 42°. Биссектрисы углов при вершинах A и B пересекаются в точке S. Определите градусную меру угла ASB. ​
Определите градусную меру суммы углов CBA+CAB

Answer 1

Ответ:

∠ ASB=111°,

∠CBA+∠CAB=138°

Объяснение:

По свойству треугольника: сумма углов треугольника равна 180°. Пусть ∠ABS=α, тогда ∠SBС=α - так как BS - биссектриса.  Значит ∠ABC=∠ABS+∠SBС. ∠ABC=2α. Выразим ∠ВАС через α и ∠BCA. Из Δ ABC получаем

∠CBA+∠CAB+∠ВСА=180°

Подставим известные значения

∠CBA+∠CAB+42°=180°

∠CBA+∠CAB=180°-42°

∠CBA+∠CAB=138°

С другой стороны, если в (1) подставить вместо  ∠CBA=∠ABC=2α, то получим

2α+42°+∠ВСА=180°

∠ВСА=138°-2α. Так как у этого угла тоже существует биссектриса, то разделим этот угол пополам.

∠СAS=∠BAS=β. C другой стороны ∠ВАС=∠СAS+∠BAS=2β.

2α+42°+2β=180°. Выразим β через α.

2β=180°-42°-2α

2β=138°-2α

β=138°:2-α

β=69°-α

Из ΔABS

∠BAS+∠ASB+∠SBA=180°

69°-α+α+∠ASB=180°

∠ASB=180°-69°

∠ASB=111°