Предмет: Алгебра,
автор: eos9215
Нужна помощь в решении неравенства с логарифмами
Приложения:
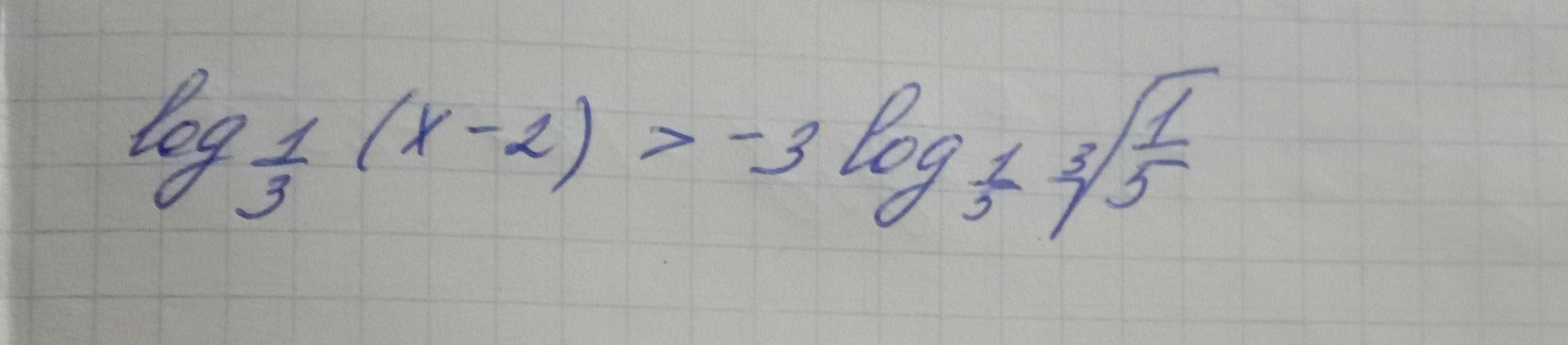
Ответы
Автор ответа:
1
Ответ:
х∈(2;7)
Объяснение:
_____________________
ОДЗ:
Подлогарифмическое выражение должно быть строго больше нуля. Если ∛(1/5) очевидно положителен, то для х-2 нужно поставить это условие.
_____________________
Если равны основания логарифмов, то равны и подлогарифмические выражения. В основании число больше единицы, значит знак не меняется.
Вместе с ОДЗ ответ получается следующим: х∈(2;7)
Похожие вопросы
Предмет: Английский язык,
автор: полинок2005
Предмет: Русский язык,
автор: artemumarovsk
Предмет: Русский язык,
автор: sokolovnick
Предмет: Химия,
автор: danilka5945
Предмет: Биология,
автор: vladimir00149