Предмет: Математика,
автор: taniabairak5
Дуже потрібно даю 30 балів, потрібно до завтра
Приложения:
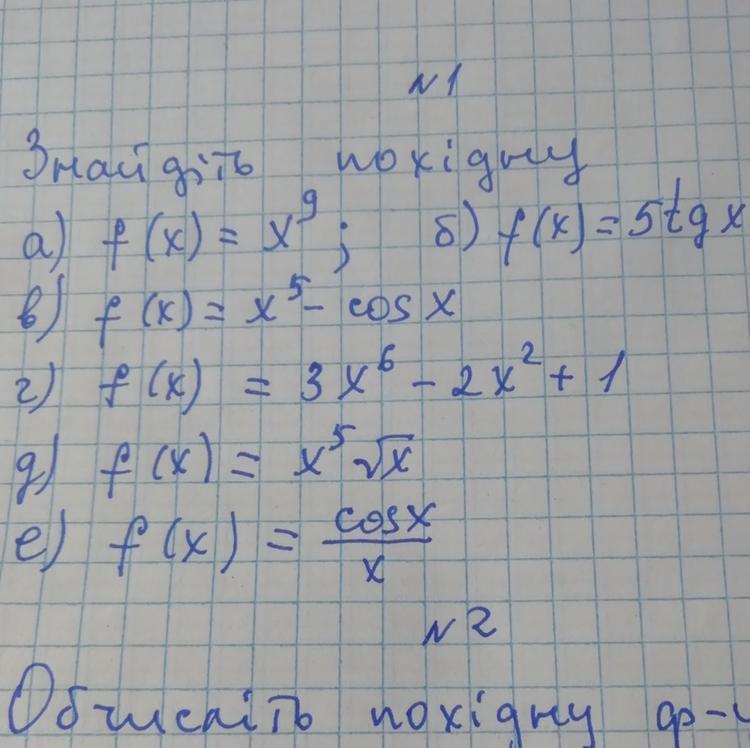
Ответы
Автор ответа:
1
Пошаговое объяснение:
Используем формулы
Так же
Найдем производные
Похожие вопросы
Предмет: Английский язык,
автор: apostrovnel
Предмет: Русский язык,
автор: серый91984043
Предмет: Другие предметы,
автор: Fox7777777777
Предмет: География,
автор: snezhanamatveeva2014
Предмет: Математика,
автор: ansar138