Question

Серединний перпендикуляр діагоналі прямокутника утворке з його більшою стороною кут 60°. Відрізок цієї прямої, який належить прямокутнику, дорівнює 12 см. Знайдіть більшу сторону прямокутника.
Допоможіть будь ласка!!!​

Answer 1

Ответ:

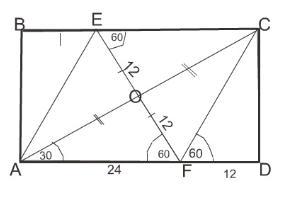
Срединный перпендикуляр к диагонали прямоугольника образует с КАЖДОЙ большей стороной угол 60°, и каждая его половина равна 12 см.

Отрезок большей стороны AF равен 24, т.к. OF=12 и противолежит углу 30°.

EF равна 24 cм (12*2) и треугольник АЕF - равнобедренный с углом при вершине 60° . Отсюда следует, что все углы этого треугольника равны 60°.

То же самое можно доказать для треугольника ЕСF.

FD противолежит углу 30° и равен 12 см.

Сторона АД=24+12=36 см

Объяснение: