Предмет: Алгебра,
автор: m1ster10
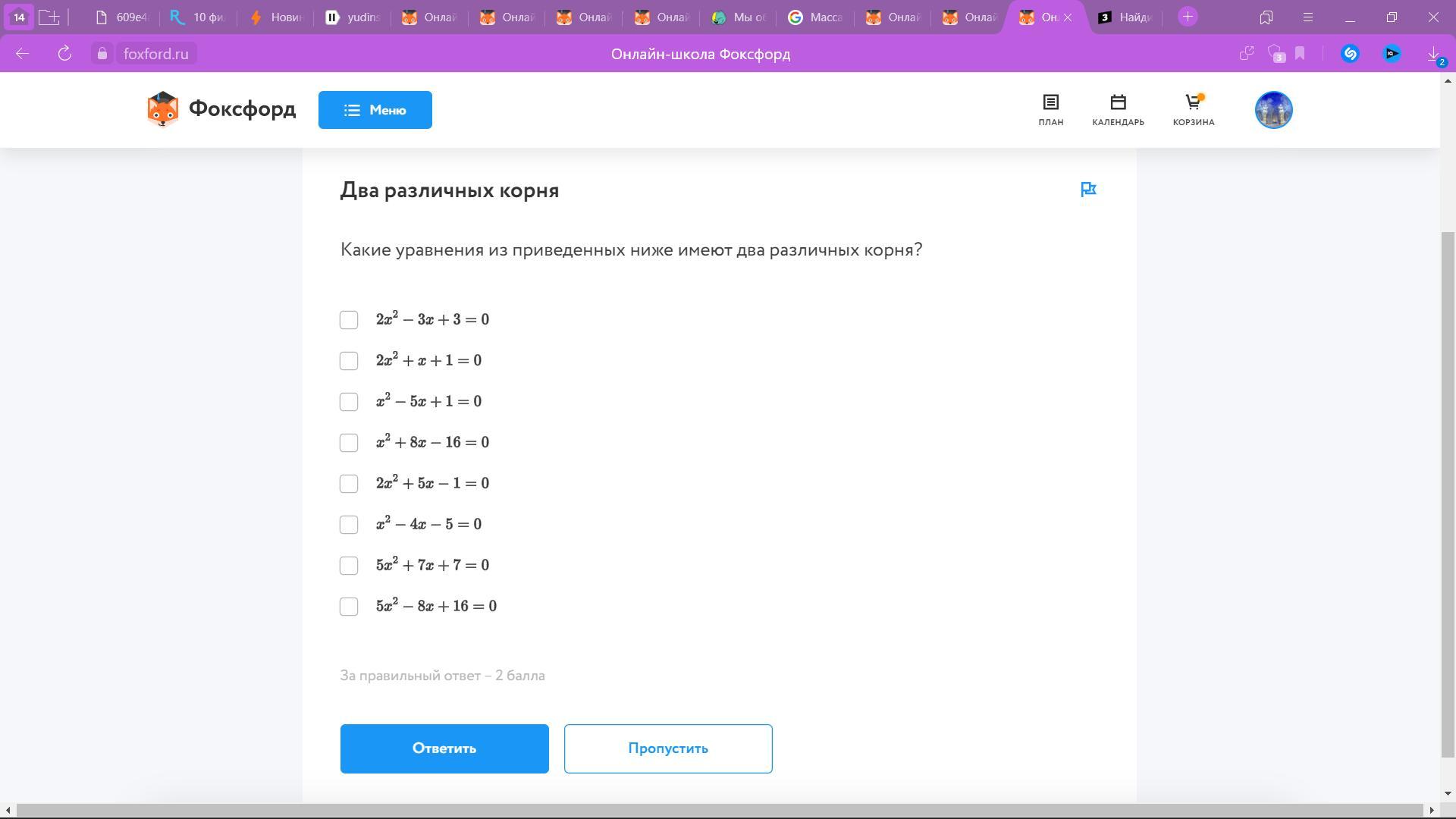
КакИЕ уравнения из приведенных ниже имеют два различных корня?
Приложения:
Mikail2006:
Я отвечу*
Ответы
Автор ответа:
5
Ответ:
Объяснение:
Квадратное уравнение имеет два различных корня, если дискриминант больше нуля (D > 0).
Формула дискриминанта ⇒
Решение:
спасибо большое ,если можешь реши еще пж ,щас будут добавляться
Пожалуйста))
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Айгерім000
Предмет: Русский язык,
автор: Ольга967
Предмет: Окружающий мир,
автор: мусипуси3
Предмет: Русский язык,
автор: ilnurka228
Предмет: Алгебра,
автор: OFFIGEVSHII