Предмет: Алгебра,
автор: AnnaTutti
Помогите решить пример во вложении
Приложения:
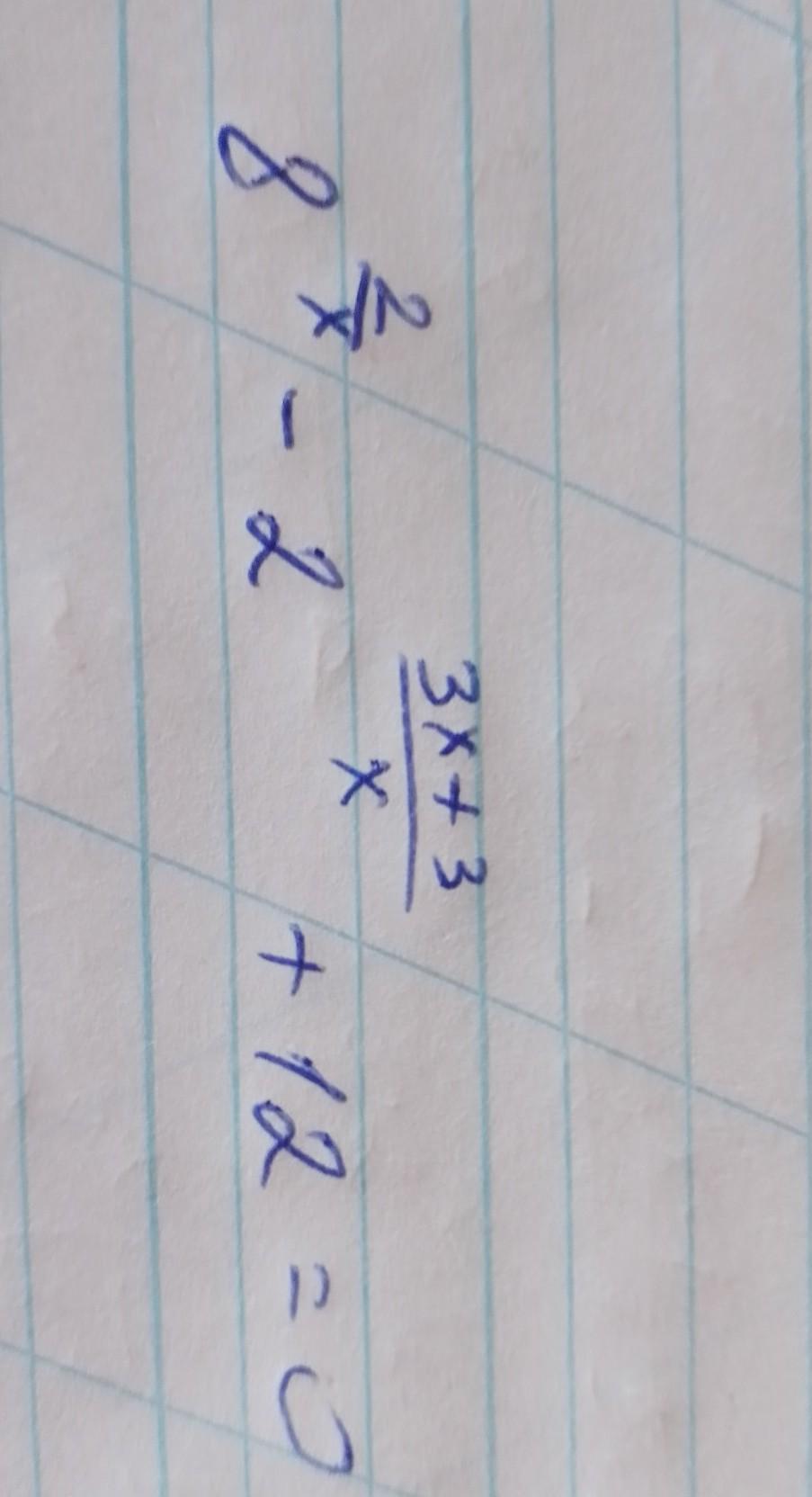
Ответы
Автор ответа:
1
( ОДЗ:
)
Замена:
(ОДЗ: t>0)
Обратная замена:
1)
2)
Ответ: {
}
Похожие вопросы
Предмет: Українська мова,
автор: DanyPro1
Предмет: Русский язык,
автор: виталий117
Предмет: Английский язык,
автор: ксюшазооо
Предмет: Математика,
автор: salazirko
Предмет: Українська мова,
автор: Unicorn13098