Предмет: Алгебра,
автор: darkis108
помогите пожалуйста алгебра 8 класс
Приложения:
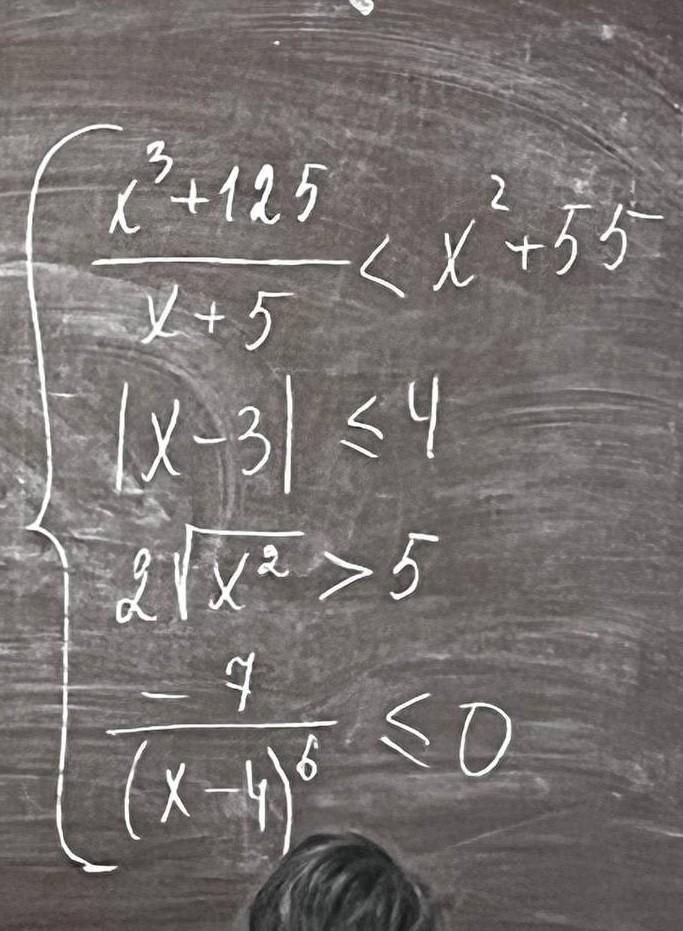
Ответы
Автор ответа:
0
Решение.
Решим по отдельности каждое неравенство .
так как знаменатель - неотрицательное выражение при любых значениях переменной х , то неравенство верно при .
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: wwwkolya2014
Предмет: Английский язык,
автор: Терька1
Предмет: Английский язык,
автор: vikusik18
Предмет: Литература,
автор: NyAsHaBrO
Предмет: Математика,
автор: farvard