Предмет: Алгебра,
автор: doonex
преобразуйте в дроби выражения (p.s. что карандашом отмечена нужно делать!)
Приложения:
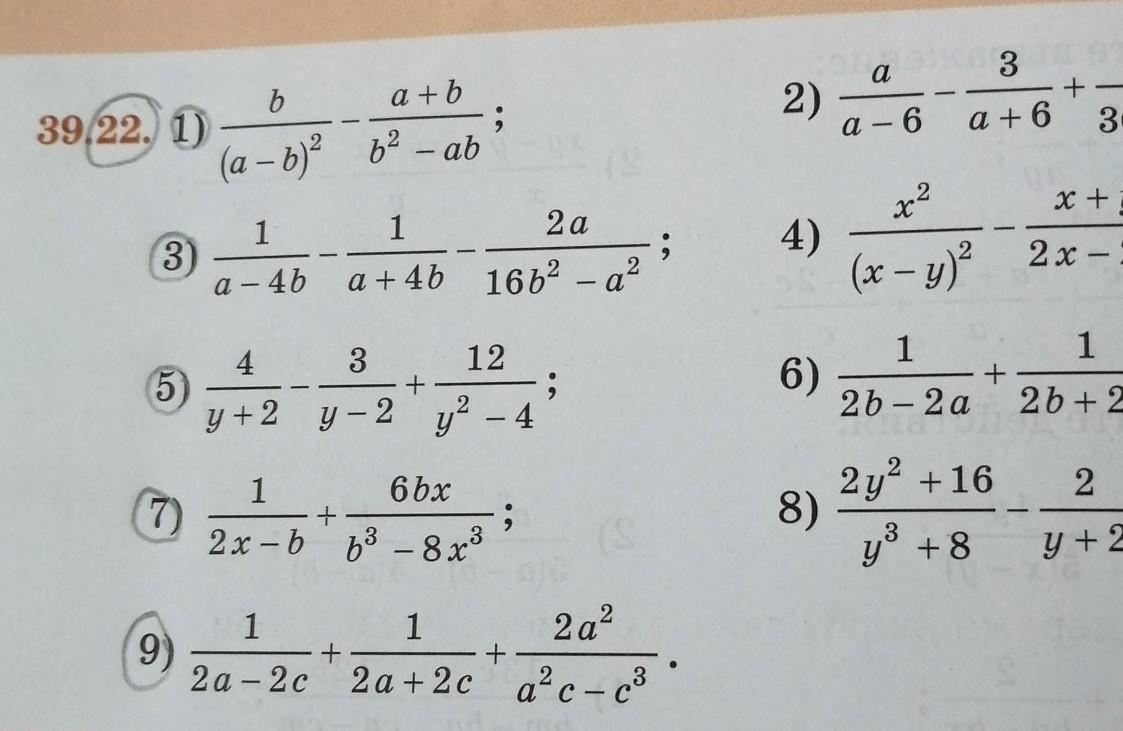
Ответы
Автор ответа:
1
Решение.
Применяем формулы сокращённого умножения.
doonex:
спасибо!
нажми на кнопки
Похожие вопросы
Предмет: Английский язык,
автор: vikusik18
Предмет: Русский язык,
автор: 7Б7
Предмет: Английский язык,
автор: daniilborodin
Предмет: Английский язык,
автор: riyad94