Исследуйте функцию и постройте график функции (найти D(f),E(f),четность и нечетность,переодичность функции,точки пересечения с осями,промежутки знако постоянства,промежутки монотонности,экстремумы функции,выпуклость и вогнутость,составить таблицу,построить график)
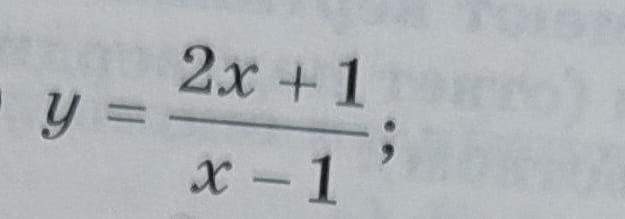
Ответы
Ответ:
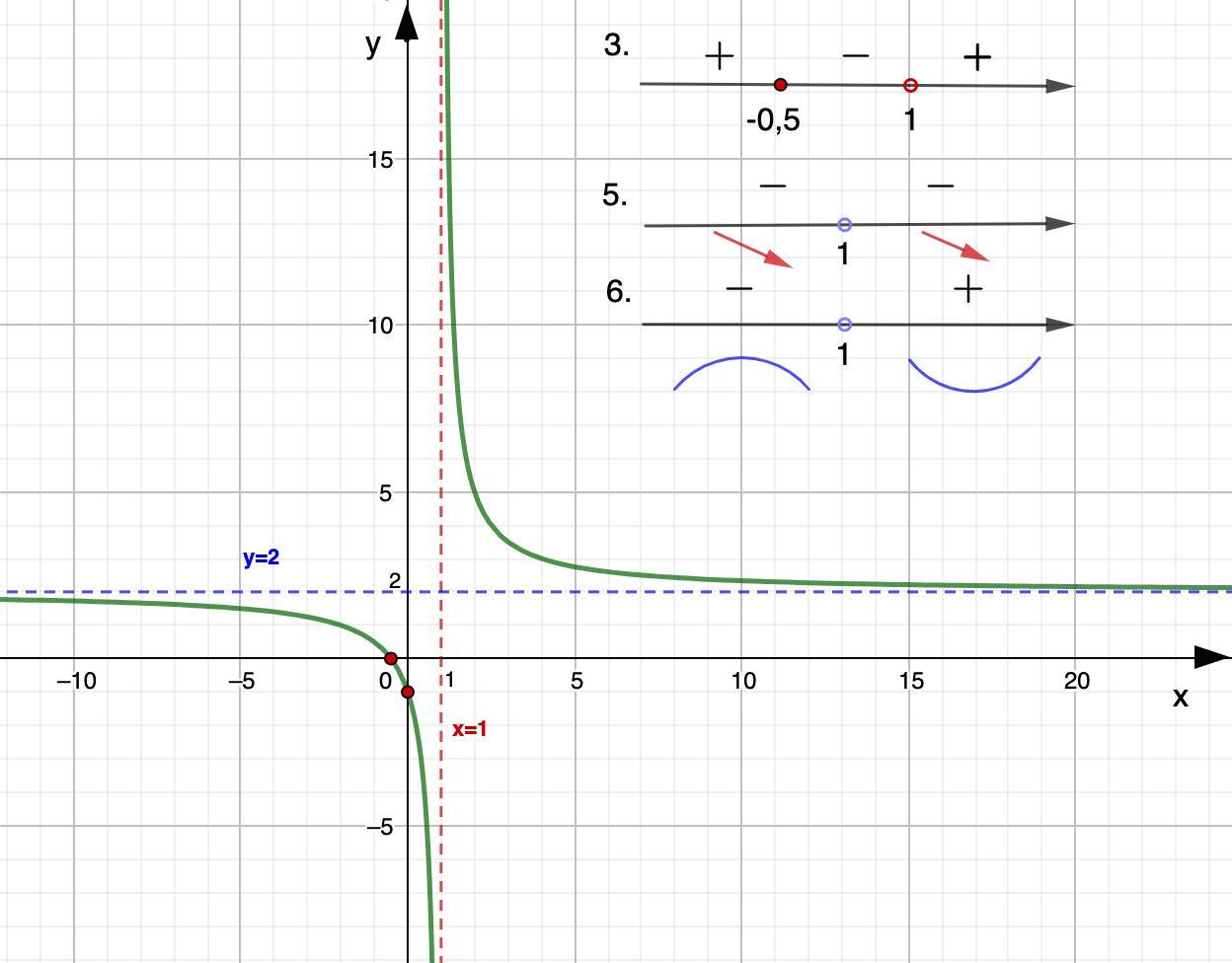
1. D(y) = (-∞; 1)∪(1; +∞)
2. функция не является четной или нечетной, непериодична.
3. пересечение с осью 0х: (-0,5; 0); с осью 0у: (0; -1)
y > 0 при х ∈ (-∞; -0,5] ∪ (1; +∞)
у < 0 при х ∈ [-0,5; 1)
4. x = 1 - вертикальная асимптота.;
y = 2 - горизонтальная асимптота.
5. Функция убывает на промежутках: (-∞; 1); (1; +∞)
Экстремумов нет.
6. Выпукла: (-∞; 1)
Вогнута: (1; +∞)
Точек перегиба нет.
Объяснение:
Исследуйте функцию и построить график функции
1. Область определения функции.
Знаменатель не равен нулю.
х - 1 ≠ 0
х ≠ 1
D(y) = (-∞; 1)∪(1; +∞)
2. Четность, нечетность, периодичность.
Если у(-х) = у(х) - функция четная; если у(-х) = -у(х) - функция нечетная.
y(-x) ≠ y(x) ≠ -y(x) ⇒ функция не является четной или нечетной.
Если y(x + T) = y (x) - функция периодична.
y(x + T) ≠ y (x) ⇒ функция непериодична.
3. Пересечение с осями, промежутки знакопостоянства.
1) с осью 0х ⇒ у = 0
(-0,5; 0)
2) с осью 0у ⇒ х=0
(0; -1)
Найдем промежутки знакопостоянства.
у > 0; y < 0.
Решим методом интервалов.
х = -0,5; х ≠ 1
(см. вложение)
4. Асимптоты.
⇒ x = 1 - вертикальная асимптота.
Наклонная асимптота: y = kx + b
⇒ y = 2 - горизонтальная асимптота.
5. Возрастание, убывание, экстремумы.
Найдем производную, приравняем к нулю и найдем корни.
Производная отрицательна, значит функция убывает, в точке х = 1 - не существует.
Функция убывает на промежутках: (-∞; 1); (1; +∞)
Экстремумов нет.
(см. вложение)
6. Выпуклость, вогнутость.
Найдем производную второго порядка.
Вторая производная не существует в точке х = 1.
Рассмотрим знаки второй производной на промежутках.
Если вторая производная положительна, функция вогнута, отрицательна - выпукла.
Выпукла: (-∞; 1)
Вогнута: (1; +∞)
Точек перегиба нет.
(см. вложение)
Строим график.
#SPJ1