Question

Решить систему линейных уравнений тремя разными способами (графическим, способом подстановки и способом алгебраической суммы): х-2y = -7,
2x + y = 1​

Answer 1

Ответ:

решение системы   $\displaystyle \boldsymbol { \left \{ {{x=-1} \atop {y=3\hfill}} \right. }$

Пошаговое объяснение:

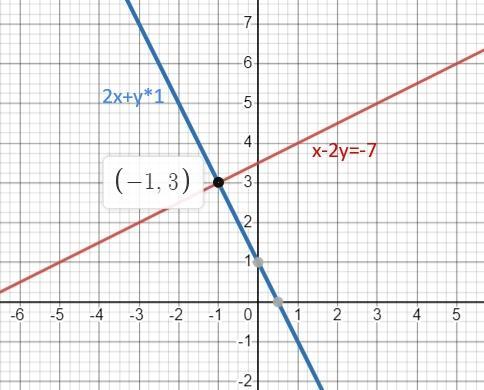
1. Графический метод

Рисуем каждый график. Обе функции - линейные. Их графики - прямые линии.

Берем для каждого по две точки и рисуем эти прямые. Точка их пересечения и есь решение системы.

2) Подстановка.

Из первого выражаем х подставляем во второе, на ходим у и потом это значение у подставляем  в первое и находим х

$\displaystyle \left \{ {{x-2y=-7} \atop {2x+y=1}} \right. \left \{ {{x=2y-7\hfill} \atop {2(2y-7)+y=1}} \right. \left \{ {{x=2y-7} \atop {5y=15\hfill}} \right. \boldsymbol {\left \{ {{x=-1} \atop {y=3\hfill}} \right. }$

3) Алгебраическая сумма

Второе умножаем на 2, складываем с первым и находим х

$\displaystyle \left \{ {{x-2y=-7\hfill} \atop {2x+y=1\hfill\quad \bigg |*2}} \right. \left \{ {{x-2y=-7} \atop {4x+2y=2\hfill}} \right.$

x - 2y +4x -+ 2y = -7+2

5x = -5

x = -1

Теперь подставляем х = -1 во второе и находим у

2*(-1) +у = 1

у= 3

решение системы   $\displaystyle \boldsymbol { \left \{ {{x=-1} \atop {y=3\hfill}} \right. }$