Предмет: Алгебра,
автор: aminamustafina15
Найдите площадь треугольника, с вершинами в точках А(4: 6),
В (2: 1), С(6; 1).
Ответы
Автор ответа:
2
Ответ:
S = 10 см^2
Объяснение:
|AB| = √((2-4)^2 + (1-6)^2) = √(4+25) = √29
|BC| = √((6-2)^2 + (1-1)^2) = √(16+0) = √16 = 4
|CA| = √((4-6)^2 + (6-1)^2) = √(4 + 25) = √29
Вычислим площадь треугольника , по формуле Герона.
p = (√29+4+√29)/2 = (2+√29)
p - полупериметр.
S = √((2+√29)×((2+√29)-√29)×((2+√29)-4)×((2+√29)-√29)) = √100 см^2 = 10 см^2
Справочный материал:
|AB| = √((xb-xa)^2 + (yb-ya)^2 + (zb-za)^2)
p = (a+b+c)/2
S = √(p(p-a)×(p-b)×(p-c))
Автор ответа:
1
Ответ: 10
Объяснение:
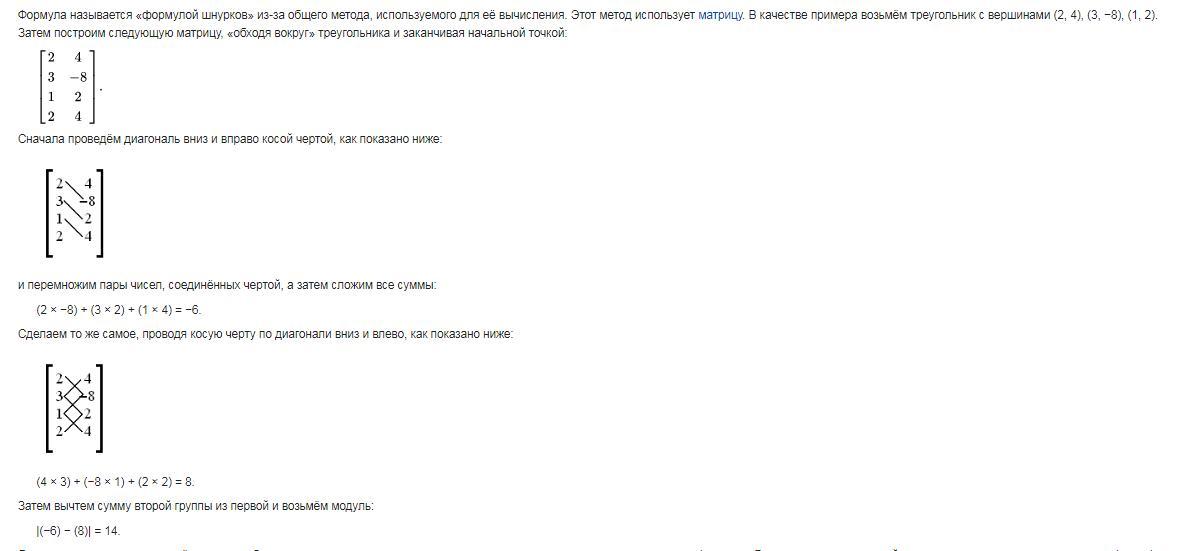
Найдем площадь с помощью формулы шнурков
Более подробный пример в приложении
Приложения:
не знала такого способа.
Очень хороший метод , с помощью него можно находить площадь даже для 20 угольников .
Похожие вопросы
Предмет: Английский язык,
автор: Йована1
Предмет: Английский язык,
автор: Anastasiawww10
Предмет: Русский язык,
автор: Konowalowjeny
Предмет: Алгебра,
автор: Летаргия888
Предмет: Алгебра,
автор: vadimsokolov3
Длина основания 6-2=4
S=1/2*4*5=10 ( ед²)