Предмет: Алгебра,
автор: LizaShaidyuk2007
Помогите решить: 1 / x^3-4x + 1 / x^3+4x - 5 / x^4-16 = 0
На фотке это первое уравнение, если что))
Приложения:
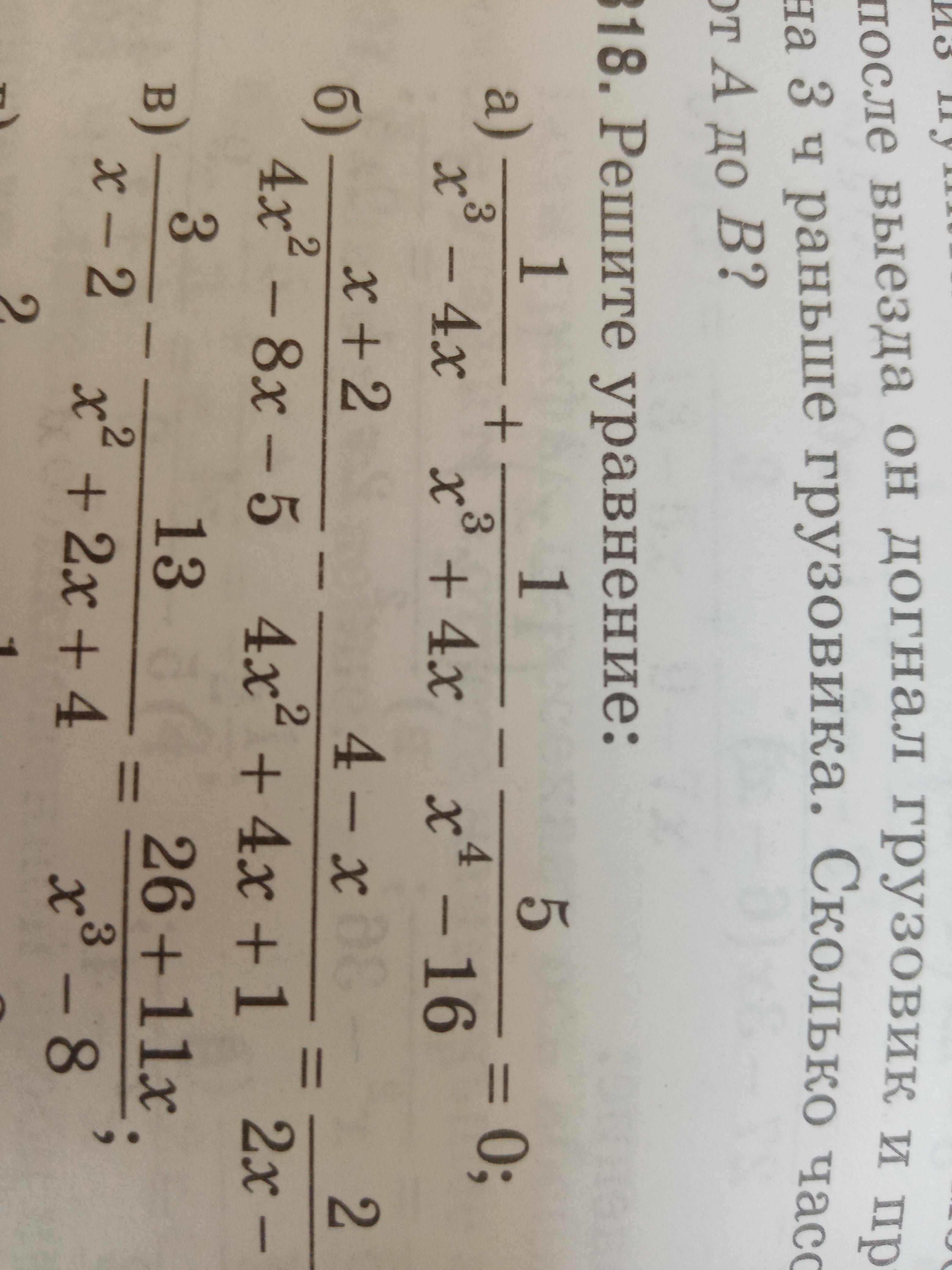
Ответы
Автор ответа:
1
Разложим числители на множители:
x^3-4x = x(x^2 - 4)
x^3 + 4x = x(x^2 + 4)
x^4 - 16 = (x^2-4)(x^2+4)
Общий знаменатель:
x(x^2-4)(x^2+4)
Тогда первую дробь домножим на (x^2 + 4), вторую - на (x^2 - 4),
третью - на x
Получим:
x^2 + 4 + x^2 - 4 -x/x(x^2-4)(x^2+4)=0
2x^2 - x / x(x^2-4)(x^2+4) = 0
x(2x-1) / x(x^2-4)(x^2+4) = 0 сократим на х
2x-1 / (x^2-4)(x^2+4) = 0
Тогда:
числитель равен нулю, знаменатель НЕ равен нулю
x = 1/2
x ≠ 2
x ≠ -2
Корни не совпадают, значит x = 1/2 = 0,5
LizaShaidyuk2007:
Ой, спасибо большое :)
Похожие вопросы
Предмет: Русский язык,
автор: Konowalowjeny
Предмет: Окружающий мир,
автор: рпщполпвп
Предмет: Английский язык,
автор: Топала007
Предмет: Физика,
автор: daniildaniltarasov
Предмет: Обществознание,
автор: galka235155