Question

РЕШИТЕ ПЛЗ БУДУ ,ОЧЕНЬ БЛАГОДАРЕН

НЕ ПО ТЕМЕ - БАН

Answer 1

$\dfrac{x^2+6x+9}{x^2-9}$

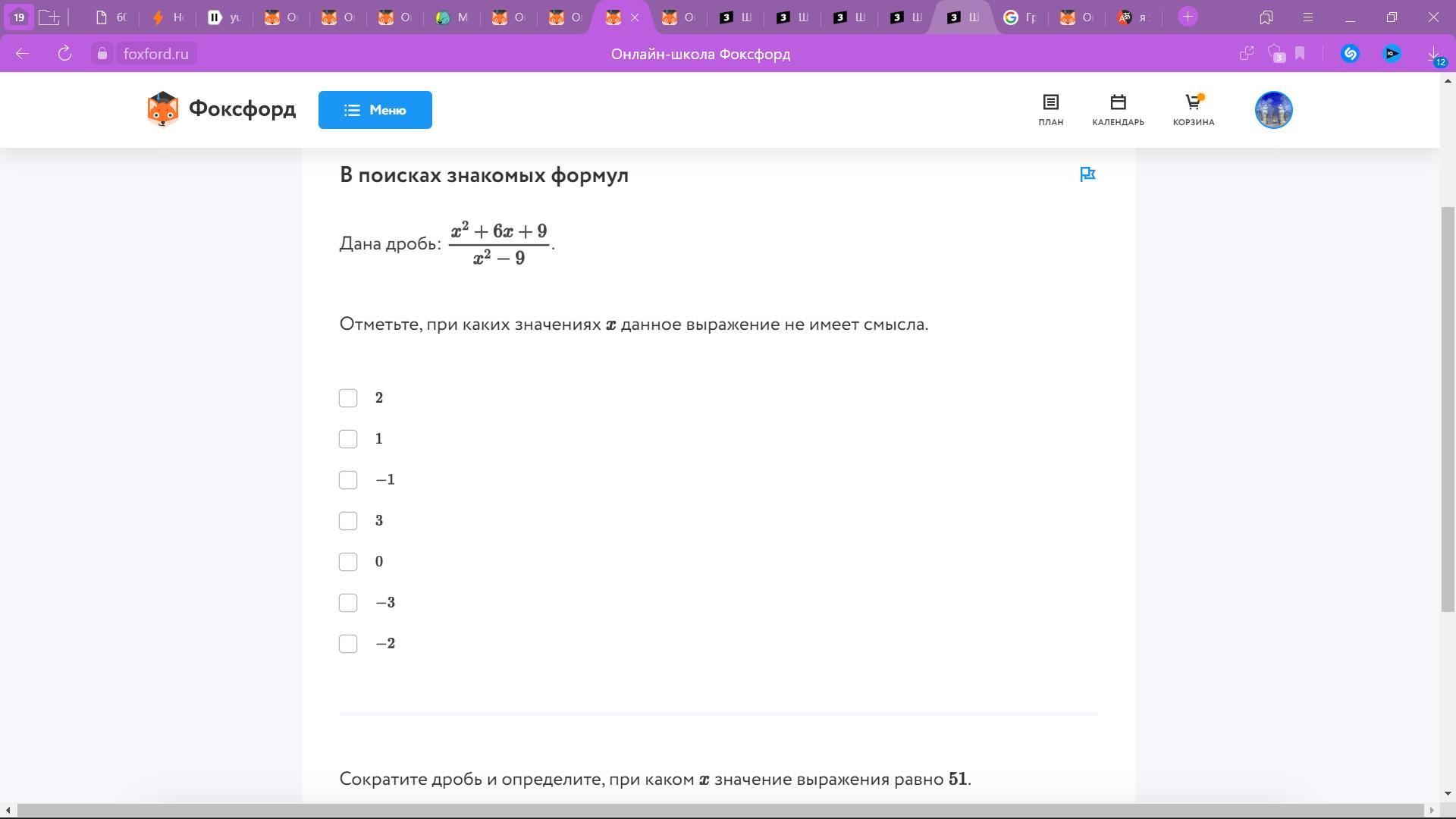
дробь не имеет смысла, если её знаменатель равен нулю

$x^2-9\ne0\\x^2\ne9\\x\ne\pm3$

ответ: 3 и -3

$\dfrac{x^2+6x+9}{x^2-9}=\dfrac{(x+3)^2}{(x-3)(x+3)}=\dfrac{x+3}{x-3}$

при этом ОДЗ не меняется: $x\ne\pm3$

$\dfrac{x+3}{x-3}=51\\\\x+3=51x-153\\50x=156\\x=3.12$

ответ:  при x = 3,12 дробь принимает значение 51

Answer 2

Ответ:   $x\ne 3\ ,\ x\ne -3\ .$

Знаменатель дроби не может быть равен 0 .

$\dfrac{x^2+6x+9}{x^2-9}\ \ \ \Rightarrow \ \ \ x^2-9\ne 0\ \ ,\ \ (x-3)(x+3)\ne 0\ \ ,\\\\\\\underline{x\ne 3\ ,\ x\ne -3}$

Данное выражение можно упростить , но ОДЗ останется таким же.

$\dfrac{x^2+6x+9}{x^2-9}=\dfrac{(x+3)^2}{(x-3)(x+3)}=\dfrac{x+3}{x-3}\ \ ,\ \ ODZ:\ x\ne 3\ ,\ x\ne -3\ .$

$b)\ \ \ \dfrac{x+3}{x-3}=51\ \ \Rightarrow \ \ \ x+3=51(x-3)\\\\x+3=51x-153\\\\50x=156\\\\x=3,12$