Предмет: Геометрия,
автор: danilfyrmanov1345
Задача на фото. С решением.
Приложения:

Ответы
Автор ответа:
0
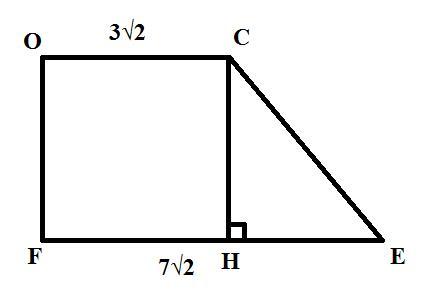
Дано:
= 50 м²
EF = 7√2 м
OC = 3√2 м
Найти:
OF и CE
Решение:
Площадь трапеции равна полусумме оснований на высоту ( S = ). Отсюда найдём высоту CH:
CH = . Подставим все известные данные:
CH = (м)
CH = OF = 5 √2 м (так как трапеция прямоугольная, её высота будет равняться одной из сторон, которая также перпендикулярна основанию)
Теперь найдём HE.
OFHC - прямоугольник (все углы прямые и противолежащие стороны параллельны). У прямоугольника противолежащие стороны равны: OC = FH = 3√2 (м). Отсюда найдём HE:
HE = FE - OC = 7√2 - 3√2 = 4√2 (м).
HE мы искали для того, чтобы рассмотреть прямоугольный треугольник CHE и по теореме Пифагора найти CE:
CE² = CH² + HE² = = 25 * 2 + 16 * 2 = 50 + 32 = 82;
CE = √82 (м)
Ответ: OF = 5√2 м; CE = √82 м
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: HeLpmepleas224
Предмет: Русский язык,
автор: Ксюшенька006
Предмет: Химия,
автор: Pro100Al002
Предмет: Математика,
автор: Egorpomidor228