Предмет: Геометрия,
автор: funpopunka
Треугольник ABC вписан в окружность радиусом 12 см. Если
Приложения:
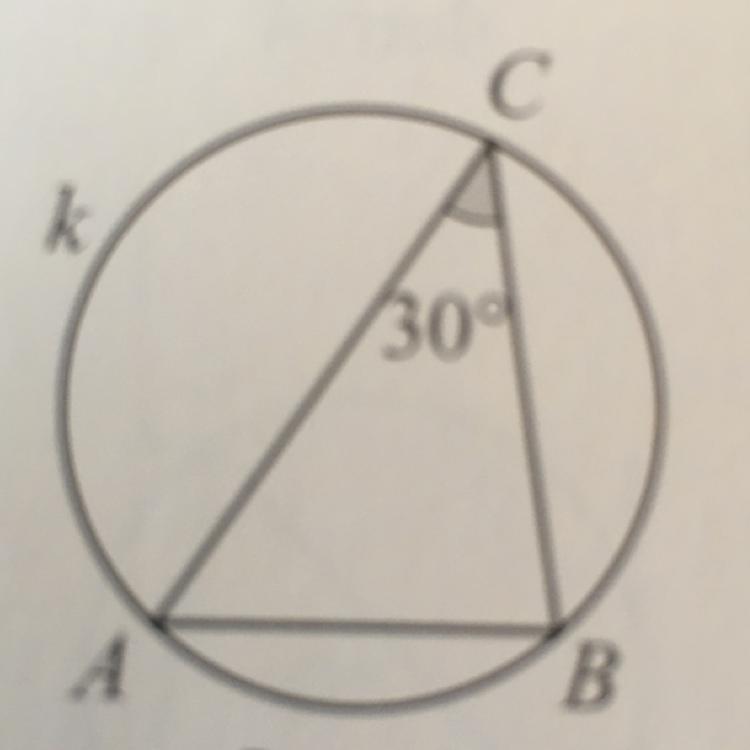
funpopunka:
Треугольник ABC вписан в окружность радиусом 12 см. Если
Почему то текст обрезался
Да бл
Если
….
Ок
Можете не помогать ведь это приложение банально не даёт мне дописать задачу
найдите длину стороны АВ
Вот что нужно
Остальное на чертеже
Ответы
Автор ответа:
1
Для решения этой задачи воспользуемся теоремой синусов:
2R = , где R - радиус описанной окружности, a - сторона треугольника, sinα - угол, лежащий напротив стороны a. В данной задаче мы выбираем сторону AB и, соответственно, синус угла C. Тогда теорема синусов будет выглядеть так:
2R = .
Выразим отсюда AB:
AB = 2R * sinC. Подставим все данные:
AB = 2 * 12 * sin30° = 24 * 0,5 = 12 (см)
Ответ: AB = 12 см
Ого, я решила её уже по другому но всё равно спасибо
Всегда найдется несколько способов решить задачу) И да, не за что! Будут вопросы, обращайтесь)
Похожие вопросы
Предмет: Русский язык,
автор: dominika0770
Предмет: Другие предметы,
автор: Tanka66
Предмет: Русский язык,
автор: fish15
Предмет: Литература,
автор: nastusha200491