Question

2. В равнобедренном треугольнике ABC с основанием AB проведена биссектриса AD. Найдите углы треугольника, если ADC=108​

Answer 1

Ответ:

∠А=∠В=72°, ∠С=36°

Пошаговое объяснение:

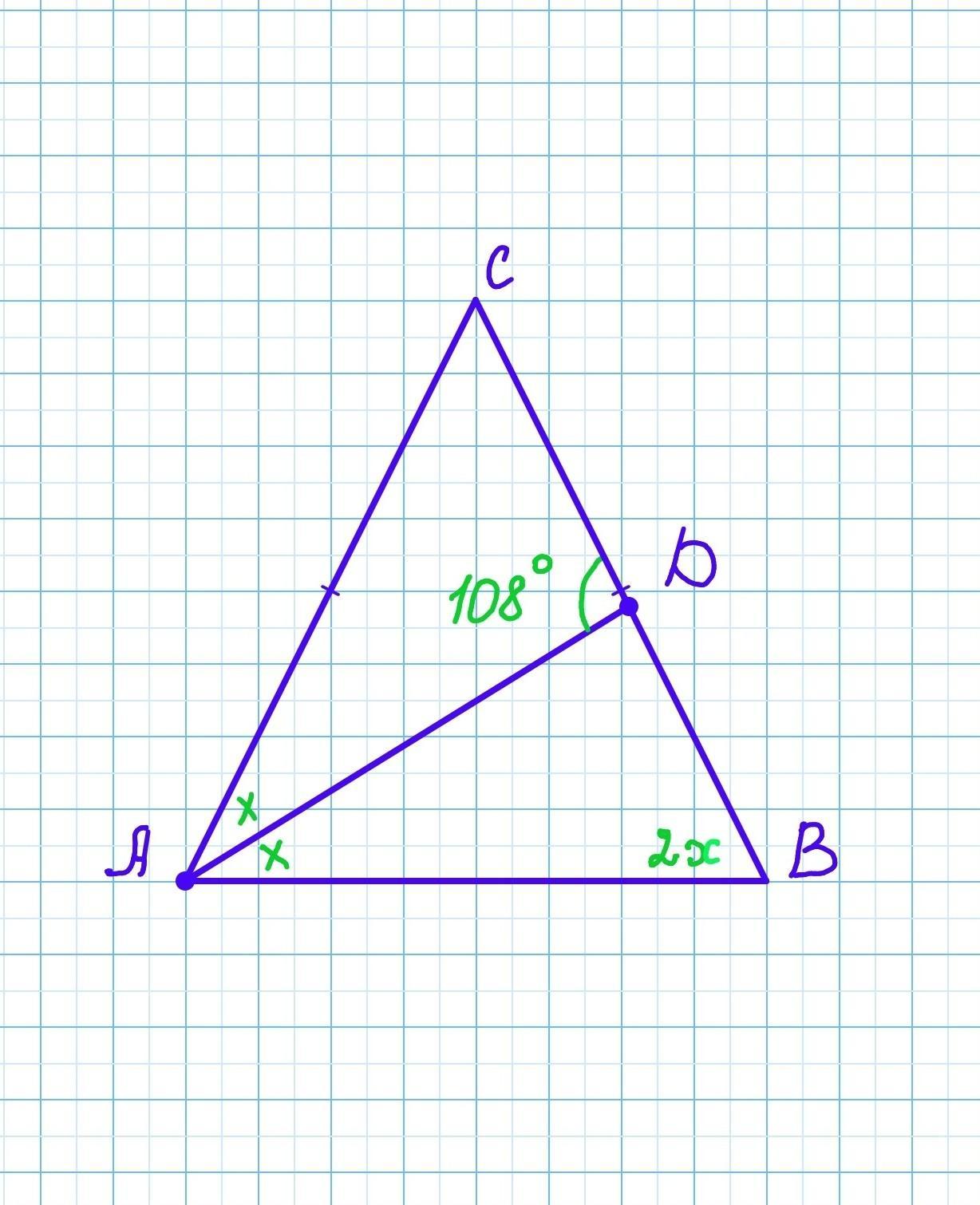
В равнобедренном △ ABC с основанием AB проведена биссектриса AD. ∠ADC=108.

Найдите углы треугольника.

Так как AD - биссектриса угла А, то ∠СAD=∠BAD= x. ∠А= 2х.

В равнобедренном треугольнике углы при основании равны, поэтому ∠В=∠А=2х

Рассмотрим △ABD.

∠ADC - внешний угол треугольника ABD.

• Внешний угол треугольника равен сумме двух других углов треугольника, не смежных с ним.

∠BAD+∠B=∠ADС

x+2x=108°

3x=108°

x=36°

Поэтому ∠А=∠В=2×36°=72°, ∠С=180°-∠А-∠В=180°-72°-72°= 36°

#SPJ1