Question

Найти объём конуса, вписанного в шар, если объём шара равен 36Пи см 3, а высота конуса равна 5 см.

Answer 1

Ответ:
35π см³
Решение:
Из формулы нахождения обьема шара:
Vш=4πR³/3; найдем радиус
R=³√(3*V/4π)=³√(3*36π/4π)=
=³√(108π/4π)=³√27=3см. радиус шара.
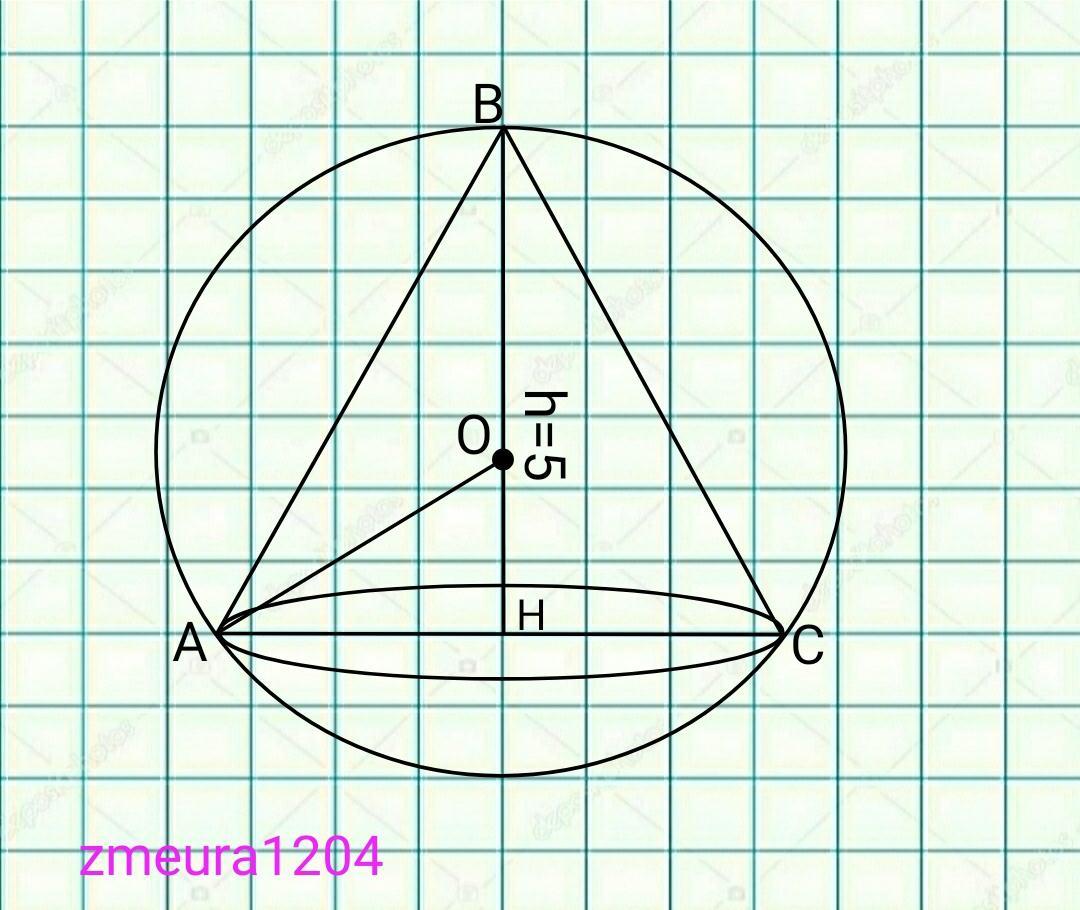
ВО=АО=R=3см
ОН=ВН-ВО=5-3=2см.
∆АОН- прямоугольный треугольник
По теореме Пифагора
АН=√(АО²-ОН²)=√(5²-2²)=
=√(25-4)=√21 см радиус конуса.(r=√21см)
Vц=⅓*πr²*h=⅓*π*(√21)²*5=
=35π см³