Question

Точка К расположена от всех сторон прямоугольного треугольника на расстоянии 26см. Высота прямоугольного треугольника, проведенная к гипотенузе 24 см и делит гипотенузу в отношении 9:16. Найдите расстояние от точки К до плоскости треугольника.

Answer 1

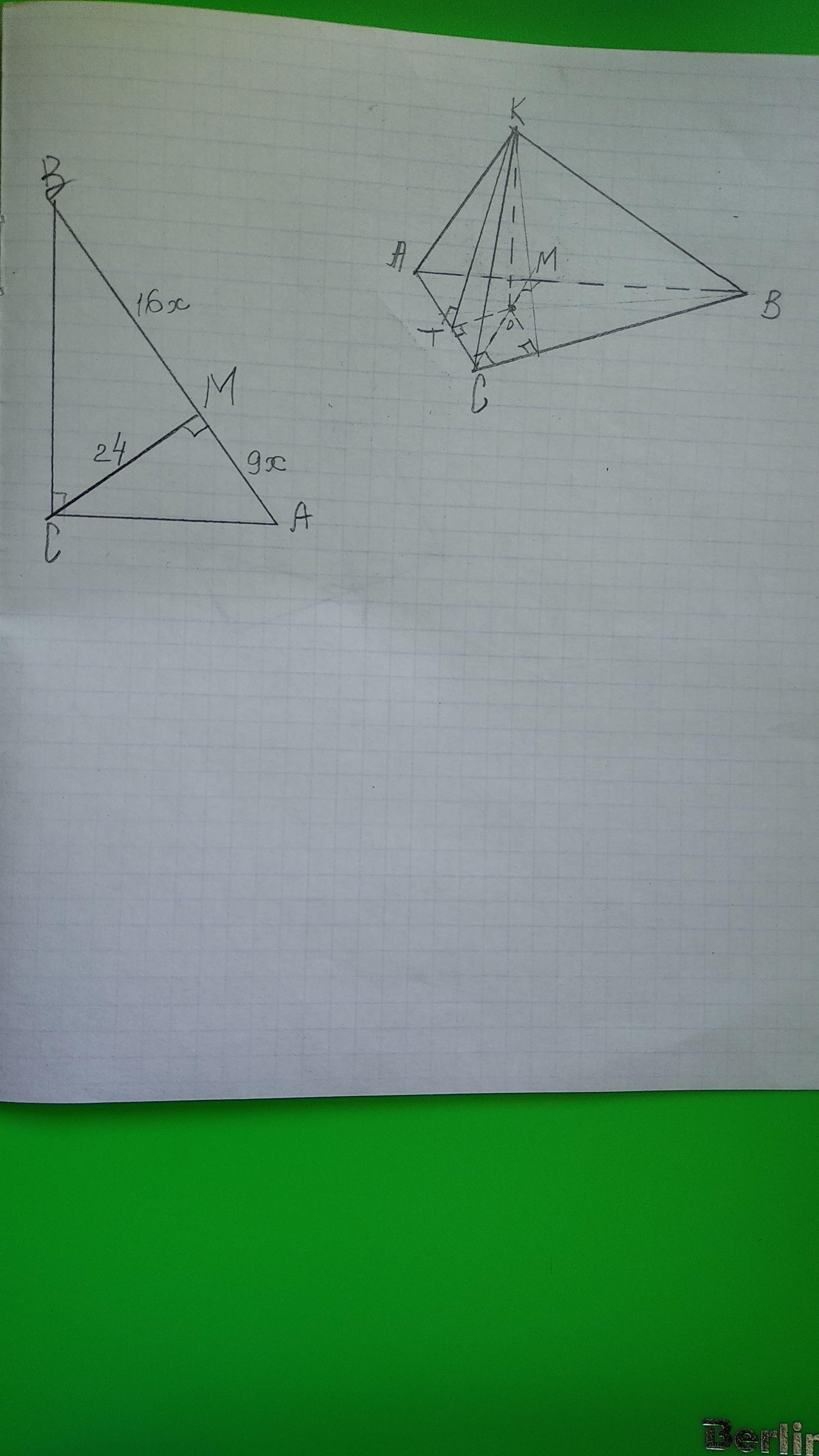
Дан трегуольник АВС (∠ С=90°, АВ=24см);  АМ:МВ=9:16;

т.к. точка К равноудалена от сторон прямоугольного треугольника АВС на расстояние КТ=26 см, то проекцией этой точки на плоскость АВС является точка О - центр окружности, вписанной в прямоугольный треугольник АВС, а радиус этой окружности ОТ может быть найден по формуле r=(АВ+ВС-АВ)/2АС

Из ΔАВС по свойству пропорциональных отрезков:

если х- коэффициент пропорциональности,то АМ=9х; ВМ=16х;

СМ²=АМ*ВМ

249х*16х

х²=24²/(9*16)

х=24/(3*4)

х=2

значит, АМ=9*2=18( см), АВ=25х=25*2=50(см); тогда АС=√(СМ²+АМ²)=√(24²+18²)=√(576+324)=30(см)

ВС=√(АВ²-АС²)=√(50²-30²)=40(см)

ОТ=(30+40-50)/2=10(см)

искомое расстояние КО=√(КТ²-ОТ²)=√(26²-10²)=√(676-100)=√576=24(см)