Предмет: Геометрия,
автор: kunasevaamina975
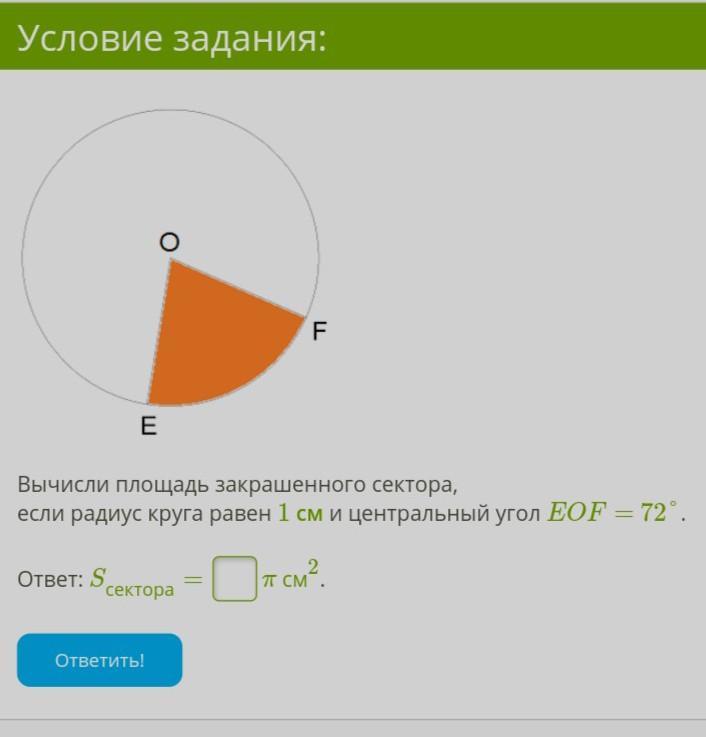
О 7. Площадь сектора. Даны ради 1 4 6 7 Список заданий Условие задания: F E Вычисли площадь закрашенного сектора, если радиус круга равен 1 см и центральный угол ЕОF = 72° . Ответ: S сектора
Приложения:
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Площадь сектора находится по формуле:
. Здесь α - мера центрального угла в радианах. Надо перевести 72° в радианы.
. Подставим значение α в формулу и найдем площадь сектора.
Похожие вопросы
Предмет: Английский язык,
автор: krasava213
Предмет: Другие предметы,
автор: zhangozy
Предмет: Английский язык,
автор: Magggrooi
Предмет: Математика,
автор: braintime2909