Предмет: Алгебра,
автор: lysokonpavel04
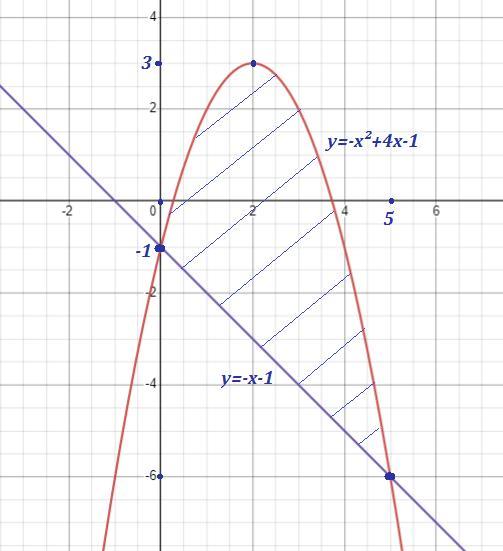
Вычислить площадь фигуры, ограниченной прямой y=ax+b и параболой y=ax^2+bx. Сделать чертёж
1) y=-x^2+4x-1, y= -x-1
Ответы
Автор ответа:
1
Решение.
Точки пересечения параболы и прямой:
Площадь фигуры равна
Приложения:
lysokonpavel04:
Правой половины не видно
Где x(x
Все вижу
Похожие вопросы
Предмет: Русский язык,
автор: baliasovaelena
Предмет: Русский язык,
автор: ks801
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: pavel4936
Предмет: Математика,
автор: JasonHostage