Предмет: Математика,
автор: rain0313
Номер 28.26
Под буквами В и Г)
Заранее большое спасибо)))
Приложения:
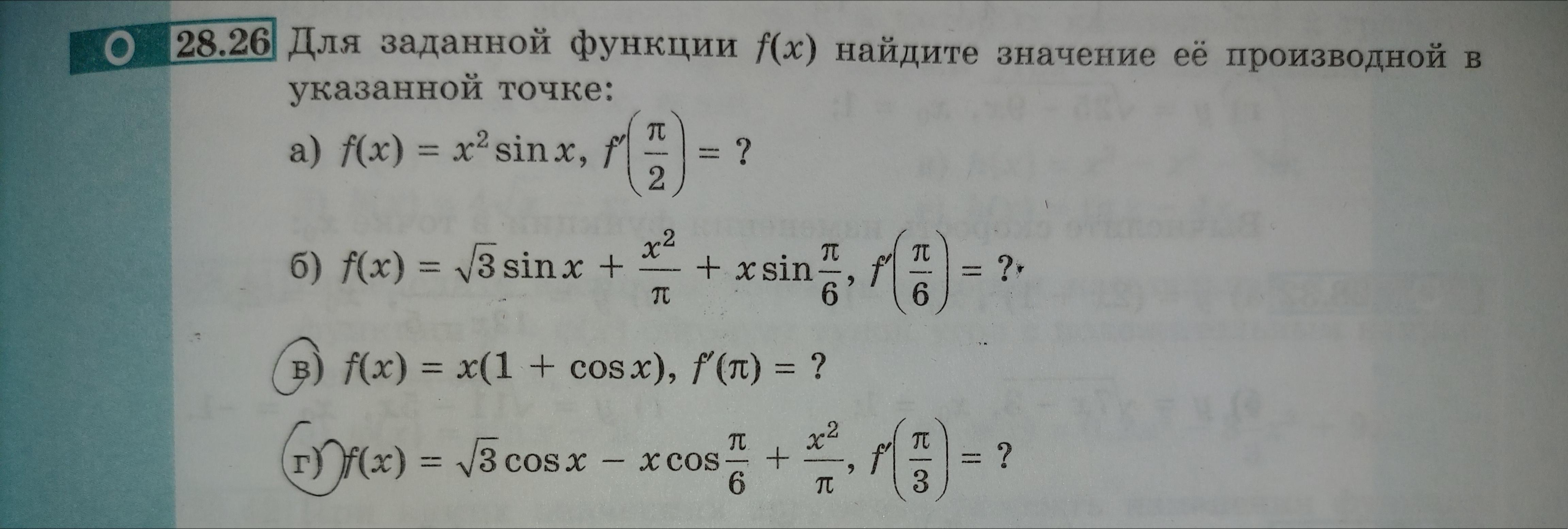
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Вспомним
Тогда
Похожие вопросы
Предмет: Русский язык,
автор: di0508di
Предмет: Русский язык,
автор: rasul56
Предмет: Русский язык,
автор: Татка028
Предмет: Биология,
автор: gugiiii
Предмет: Геометрия,
автор: Ручка1337помощник