Предмет: Алгебра,
автор: kredrok
Помогите решить пожалуйста эти примеры кому не сложно
Приложения:
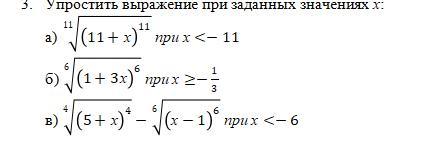
Ответы
Автор ответа:
1
Ответ:
а) На подкоренное выражение корня нечётной степени ограничения не накладывают.
б) На подкоренное выражение корня чётной степени ограничения накладывают. Подкоренное выражение должно быть неотрицательным . И действует правило . Если выражение под знаком модуля неотрицательно, то модуль равен этому выражению . Если выражение под знаком модуля отрицательно, то модуль равен противоположному выражению .
в) Решаем аналогично.
Похожие вопросы
Предмет: Английский язык,
автор: Маргоша890
Предмет: Английский язык,
автор: lelja3
Предмет: Русский язык,
автор: самира20161
Предмет: География,
автор: fgdhbvc76354
Предмет: Алгебра,
автор: dasew12